向量数据库概述

向量数据库是为处理高维向量数据而设计的数据库系统，它能够高效地存储、索引和查询大规模的高维向量数据。与关系型数据库或文档数据库相比，向量数据库在处理高维数据时具有明显优势，特别是在相似度搜索方面。向量数据库采用专门的数据结构和算法，如KD-Tree、球树、LSH等，以提高存储效率和查询性能。此外，向量数据库还支持基于相似度的查询，使用余弦相似度或欧氏距离等度量方法，实现快速准确的搜索。向量数据库广泛应用于图像和视频检索、文本语义搜索、推荐系统等领域。

索引结构

向量数据库使用多种索引结构来优化数据存储和检索。以下是一些常见的索引结构：

KD-Tree

KD-Tree是一种二叉树结构，用于高效存储和检索k维向量数据。它通过在不同维度上划分空间，将数据点分布在树的节点上。

Ball Tree

Ball Tree使用球体划分空间，适用于非均匀分布的数据集，适合处理包围球和半径搜索查询。

R-Tree

R-Tree是一种多维索引结构，适用于空间对象的组织和检索，支持范围查询和动态数据操作。

Cover Tree

Cover Tree通过将数据点放置在距离的指数级别上构建树结构，用于高维近邻搜索，具有优良的时间和空间复杂度。

VP-Tree

VP-Tree通过选择代表点作为分割点构建树形结构，适用于高维近邻搜索和范围搜索。

LSH（Locality Sensitive Hashing）

LSH是一种基于哈希的索引算法，用于大规模数据集的近似近邻搜索，具有较好的可扩展性。

索引结构优缺点分析

以下是对上述索引结构的优缺点分析：

  • KD-Tree: 优点包括高效的最近邻查询和范围搜索，适用于低维数据集；缺点是高维数据集性能下降，不支持动态操作。

  • Ball Tree: 优点是适用于非均匀分布的数据集；缺点是构建和查询速度较慢，内存需求大。

  • R-Tree: 优点是支持范围查询和动态操作；缺点是高维数据集性能下降。

  • Cover Tree: 优点是构建和查询效率高；缺点是构建复杂，不适用于范围查询。

  • VP-Tree: 优点是适用于高维近邻搜索；缺点是构建复杂，与数据分布和度量相关。

  • LSH: 优点是适用于大规模数据集，具有可扩展性；缺点是查询结果可能存在误差。

维度灾难与解决方案

维度灾难是指在高维空间中数据点间距离变得稀疏，导致查询性能下降的问题。解决维度灾难的方法包括：

  • 数据预处理和特征选择

  • 维度约减技术，如PCA、LDA、t-SNE

  • 局部敏感哈希（LSH）

  • 改进的索引结构，如M-Tree、VA-File

  • 近似算法，如近似最近邻（ANN）

KD-Tree结构详解

KD-Tree的结构是通过在每个维度上交替划分空间来构建的。在二维KD-Tree中，首先根据X轴划分数据，然后根据Y轴继续划分，形成树状结构。每一层的划分都是基于当前层的维度，从而实现高效的数据检索。

                    Node
                 /         \
           left            right
          /     \        /      \
 Nodes...  Node  Node   Node    Node

KD树是一种特殊的数据结构，用于在多维空间中进行高效地搜索和排序。它是一种二叉树，每个节点代表一个数据点，这些数据点通常是多维向量。以下是对KD树结构的详细描述：

KD树概述KD树是一种二叉树结构，它在数据点的多维空间中进行划分。树的根节点位于顶部，并且每个节点都具有两个子节点：左子节点和右子节点。

节点划分机制在KD树中，节点的划分是基于划分轴的。划分轴在树的每层中按维度循环，从而实现对数据点的多维划分。具体来说：

  • 左子节点包含所有小于当前节点的向量数据点。
  • 右子节点包含所有大于当前节点的向量数据点。

节点信息每个KD树节点包含以下关键信息：

  • point：表示节点所代表的多维向量数据点。
  • axis：表示当前节点使用的划分轴的索引。
  • left：指向左子树，包含较小的数据点。
  • right：指向右子树，包含较大的数据点。

KD树的实际结构KD树的实际形态取决于数据集中的数据点分布以及划分轴的选择。不同的数据集和划分策略会导致KD树具有不同的形状和层次结构。

三维KD树示例如果我们将KD树在三维空间中进行可视化，可以想象成一个立方体，其中每个节点代表一个立方体的角点。然而，由于是三维展示，实际的图画可能并不完美，但可以提供一个直观的理解。

（此处可以插入一个立方体的示意图，但由于文本限制，无法展示图形。） 请注意，KD树的构建和使用需要考虑数据点的分布特性，以及如何选择合适的划分轴来优化搜索效率。
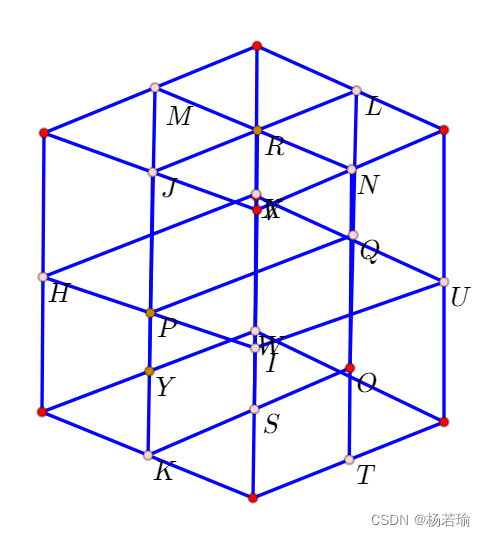
在这里插入图片描述

一个简单的KD-Tree例子

我们现在实现一个存储向量的KD-Tree：

1

import java.util.Comparator; class Node { double[] point; // 向量数据点 int axis; // 划分轴 Node left; // 左子树 Node right; // 右子树 public Node(double[] point, int axis) { this.point = point; this.axis = axis; this.left = null; this.right = null; } } public class KDTree { private Node root; // 根节点 private int k; // 数据点的维度 public KDTree(int k) { this.root = null; this.k = k; } private Comparator<double[]> comparator = new Comparator<double[]>() { @Override public int compare(double[] p1, double[] p2) { return Double.compare(p1[k], p2[k]); } }; public void build(double[][] points) { this.root = buildTree(points, 0); } private Node buildTree(double[][] points, int axis) { if (points == null || points.length == 0) { return null; } int median = points.length / 2; double[][] sortedPoints = sortPoints(points, median, axis); Node node = new Node(sortedPoints[median], axis); node.left = buildTree(Arrays.copyOfRange(sortedPoints, 0, median), (axis + 1) % this.k); node.right = buildTree(Arrays.copyOfRange(sortedPoints, median + 1, sortedPoints.length), (axis + 1) % this.k); return node; } private double[][] sortPoints(double[][] points, int median, int axis) { Arrays.sort(points, comparator); return points; } public double[] search(double[] target) { return searchNode(this.root, target); } private double[] searchNode(Node node, double[] target) { if (node == null) { return null; } if (Arrays.equals(node.point, target)) { return node.point; } if (target[node.axis] < node.point[node.axis]) { return searchNode(node.left, target); } else { return searchNode(node.right, target); } } }

首先我们定义了一个 Node 类，表示 KD 树中的节点。每个节点有以下属性：point 表示向量数据点，axis 表示划分轴的索引， left 和 right 分别表示左子树和右子树。

然后定义了 KDTree 类，表示 KD 树。每个 KD 树对象包含一个根节点 root 和数据点的维度 k。

在 KDTree 类中，通过构造函数初始化 KD 树的维度 k 和根节点 root。并且使用比较器 comparator 对数据点进行排序，以便在建树时进行划分。

build 方法用于构建 KD 树。它使用递归的方式，通过 buildTree 方法来构建树。buildTree 方法接收一个 points 参数，表示要构建树的数据点集合。根据当前轴 axis 的值将数据点集合划分成左子树和右子树，并创建当前节点，然后递归构建左右子树。

sortPoints 方法使用比较器 comparator 对输入的点集进行排序，并返回排序后的结果。

search 方法用于搜索与目标点最相似的数据点。它调用 searchNode 方法，在树中递归搜索节点。searchNode 方法首先检查当前节点是否为目标点，如果是则返回当前节点，否则根据目标点在当前轴的值与节点进行比较，决定继续在左子树或右子树中搜索。

然后我们去尝试使用一下：

1

public class KDTreeDemo { public static void main(String[] args) { double[][] points = { {2, 3}, {4, 5}, {6, 9} }; double[] target = {4, 6}; KDTree tree = new KDTree(2); tree.build(points); double[] result = tree.search(target); if (result != null) { System.out.println("找到"); } else { System.out.println("未找到"); } } }

KD-Tree在企业人员调度中的应用

在企业级领域，KD-Tree算法可以被应用于各种场景，其中之一就是人员调度问题。以下内容将详细介绍如何利用KD-Tree解决企业中的排班调度问题。

问题背景

企业在运作过程中，经常需要根据项目需求和员工的个人能力进行合理的排班调度。这涉及到员工技能和可用时间段的匹配问题。

KD-Tree简介

KD-Tree，即K-Dimensional Tree，是一种用于组织点在K维空间中的数据结构，常用于多维搜索问题。它通过递归地将空间分割成多个区域，以实现快速搜索。

应用场景分析

员工技能与时间信息的存储首先，需要将每个员工的技能和可用时间信息存储在KD-Tree中。员工的每个技能可以作为一个维度，而可用时间段则可以作为另一个维度。这样，每个员工的信息就可以在KD-Tree中得到有效的组织。

项目需求与时间匹配当企业有新的项目需求时，可以通过KD-Tree快速检索出符合项目技能要求和时间要求的员工。通过定义搜索范围，KD-Tree可以迅速缩小搜索范围，提高匹配效率。

排班调度的优化使用KD-Tree进行排班调度，不仅可以快速找到合适的员工，还可以通过调整搜索参数，优化排班方案，以达到资源的最优分配。

结论KD-Tree在企业人员调度中的应用，可以大大提高排班效率和准确性，帮助企业更好地管理人力资源，满足项目需求。

1

import java.util.Arrays; class Employee { private String name; private double[] skills; private double[] availableTime; public Employee(String name, double[] skills, double[] availableTime) { this.name = name; this.skills = skills; this.availableTime = availableTime; } // Getters and setters } public class EmployeeScheduler { private KDTree kdTree; public EmployeeScheduler() { this.kdTree = new KDTree(2); // 假设员工的技能维度为2 } public void addEmployee(Employee employee) { double[] point = new double[2]; // 假设技能维度为2 point[0] = employee.getSkills()[0]; // 技能维度1 point[1] = employee.getSkills()[1]; // 技能维度2 kdTree.insert(point); } public String findBestEmployee(double[] requiredSkills) { double[] result = kdTree.search(requiredSkills); // 根据目标点找到最适合的员工 if (result != null) { // 根据得到的点反向查找对应的员工 Employee bestEmployee = getEmployeeByPoint(result); return bestEmployee.getName(); } else { return null; } } private Employee getEmployeeByPoint(double[] point) { // 遍历员工列表，找到与给定点匹配的员工 // 根据实际情况，可以使用哈希表或其他数据结构来提高搜索效率 // 这里简化处理直接遍历 for (Employee employee : employeeList) { double[] employeePoint = new double[2]; employeePoint[0] = employee.getSkills()[0]; // 技能维度1 employeePoint[1] = employee.getSkills()[1]; // 技能维度2 // 判断两个点是否相等或匹配，这里按需求实现 if (Arrays.equals(point, employeePoint)) { return employee; } } return null; } }

向量数据库概述

向量数据库是一种新型数据库技术，它在大数据和人工智能的背景下应运而生。本文将探讨向量数据库的基本原理、应用场景以及未来的发展趋势。

基本原理

在向量数据库中，数据以多维向量的形式存储。例如，员工的技能和可用时间可以用double[]数组表示，并通过KD-Tree等数据结构进行索引。这种结构支持高效的相似性搜索和精确匹配查询。

技能与可用时间的索引

  • 技能向量插入：将员工的技能向量插入KD-Tree中，以便于后续的搜索操作。
  • 搜索匹配员工：根据所需的技能向量进行搜索，找到最适合的员工。

向量数据库的复杂性

  • 多维度处理：对于多维度的向量问题，可以改变数据表示、修改比较策略或使用不同的距离度量方法。

模糊性与确切性结果

向量数据库可以提供两种类型的查询结果：模糊性结果和确切性结果。

确切性结果（Exact Results）

  • 定义：与查询向量完全匹配的向量数据点。
  • 应用场景：
  • 数据去重
  • 数据验证
  • 精确匹配搜索

模糊性结果（Fuzzy Results）

  • 定义：与查询向量相似度高于设定阈值的向量数据点。
  • 应用场景：
  • 相似性搜索
  • 探索和发现

向量数据库的应用

向量数据库在多个领域有着广泛的应用，包括但不限于：

  • 图像和视频检索
  • 文本语义搜索
  • 推荐系统
  • 工业物联网
  • 生物信息学

发展趋势

随着人工智能和大数据的快速发展，向量数据库的发展潜力巨大。未来的向量数据库将：

  • 不断改进存储、索引和查询技术。
  • 可能与其他数据库类型混合使用，以支持更丰富的查询和分析需求。

结论

向量数据库为处理大规模高维向量数据提供了有效的解决方案，对于数据工程师、机器学习工程师和研究人员来说，学习和掌握向量数据库技术是非常有价值的。