LDA模型及其背景介绍

模型概述

LDA（Latent Dirichlet Allocation），即潜在狄利克雷分配，是一种用于发现大型文本集合中隐藏主题结构的主题模型。自2002年被提出以来，LDA已经成为分析文本信息的标准工具，并衍生出了多种应用于不同数据类型的变种模型。

发展历史

• 论文发表：LDA由David Blei、Andrew Ng和Michael Jordan提出，最初在2002年的NIPS会议上发布，完整版本于2003年发表在《Journal of Machine Learning Research》上。

• 引用量：该论文获得了超过19,000次的引用，成为机器学习领域的重要文献之一。

作者简介

• David Blei：LDA论文的主要贡献者之一，目前是哥伦比亚大学的教授，专注于统计学和计算机科学的研究。

• Andrew Ng：深度学习领域的先驱之一，曾发起Google Brain项目，创立在线教育平台Coursera。

• Michael Jordan：机器学习界的泰斗，加州大学伯克利分校教授，拥有极高的学术地位和广泛的影响力。

LDA模型详解

LDA属于产生式模型（Generative Model），与判别式模型（Discriminative Model）相对，它试图同时对特征X和标签Y进行建模，更适合无监督学习任务如聚类。

LDA的生成过程

LDA通过以下步骤描述文档及其单词的生成过程：

• 文档长度生成：从全局泊松分布（参数为β）中抽取每个文档的长度N。

• 主题分布生成：根据全局狄利克雷分布（参数为α）为当前文档生成主题分布θ。

• 单词生成：对于文档中的每一个位置n（1到N），执行以下操作：

• 从以θ为参数的多项分布中抽取一个主题下标z_n。

• 根据主题z_n，从以φ为参数的多项分布中生成单词w_n。 注意：上述生成过程是对实际数据生成机制的一种理想化假设，帮助我们理解LDA如何模拟文档和词汇之间的关系。
  

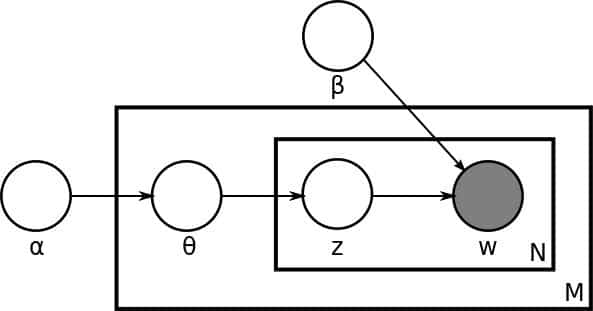
从这个描述我们可以马上得到这些重要的模型信息。第一，我们有一个维度是 K 乘以 V 的主题矩阵（Topic Matrix）。其中每一行都是一个φ，也就是某一个生成字的多项分布。当然，这个主题矩阵我们在事先并不知道，是需要学习得到的。另外，对每一个文档而言，θ是一个长度为 K 的向量，用于描述当前文档在 K 个主题上的分布。产生过程告诉我们，我们对于文档中的每一个字，都先从这个θ向量中产生一个下标，用于告诉我们现在要从主题矩阵中的哪一行去生成当前的字。

这个产生模型是原论文最初提出的，有两点值得注意。

第一，原始论文为了完整性，提出了使用一个泊松分布来描述文档的长度这一变化信息。然而，从模型的参数和隐变量的角度来说，这个假设并不影响整个模型，最终作者在文章中去除了这个信息的讨论。在主题模型的研究中，也较少有文献专注这个信息。

第二，原始论文并没有在主题矩阵上放置全局的狄利克雷分布作为先验概率分布。这一缺失在后续所有的主题模型文献中得到修正。于是今天标准的 LDA 模型有两类狄利克雷的先验信息，一类是文档主题分布的先验，参数是α，一类是主题矩阵的先验，参数是β。

文章作者们把这个模型和当时的一系列其他模型进行了对比。比如说，LDA 并不是所谓的狄利克雷 - 多项（Dirichlet-Multinomial）聚类模型。这里，LDA 对于每个文档的每一个字都有一个主题下标。也就是说，从文档聚类的角度来看，LDA 是没有一个文档统一的聚类标签，而是每个字有一个聚类标签，在这里就是主题。这也是 LDA 是Mixed-Membership 模型的原因——每个字有可能属于不同的类别、每个文档也有可能属于不同的类别。

LDA 很类似在 2000 年初提出的另外一类更简单的主题模型——概率隐形语义索引（Probabilistic Latent Semantic Indexing），简称PLSI。其实从本质上来说，LDA 借用了 PLSI 的基本架构，只不过在每个文档的主题分布向量上放置了狄利克雷的先验概率，以及在主题矩阵上放置了另外一个狄利克雷的先验概率。

尽管看上去这是一个非常小的改动，但是这样做的结果则是 LDA 的参数个数并不随着文档数目的增加而增加。那么，相对于 PLSI 来说，LDA 并不容易对训练数据过度拟合（Overfitting）。

值得注意的，原始文章说过度拟合主要是指，对于 PLSI 而言，文档的主题分布向量是必须需要学习的，而这个向量对于 LDA 是可以被忽略或者说是并不需要保存的中间变量。然而在实际的应用中，我们其实常常也需要这个向量的信息，因此这部分对于过度拟合的讨论在后来的应用中并没有特别体现。

LDA 模型的训练和结果

LDA 虽然从某种意义上来说仅仅是在 PLSI 上增加了先验信息。然而，这一个改动为整个模型的训练学习带来了非常大的挑战。应该说，整个 LDA 的学习直到模型提出后近 10 年，才随着**随机变分推理（Stochastic Variational Inference）的提出以及基于别名方法（Alias Method）**的抽样算法（Sampling Method）而得以真正的大规模化。一直以来，LDA 的训练学习都是一件很困难的事情。

不像 PLSI 可以依靠最大期望（EM）算法得以比较完美的解决，传统上，LDA 的学习属于贝叶斯推理（Bayesian Inference），而在 2000 年代初期，只有马尔科夫蒙特卡洛（Markov chain Monte Carlo），简称 MCMC，以及迈克尔·乔丹等人推崇的变分推理（Variational Inference），简称 VI，作为工具可以解决。这篇文章因为出自迈克尔的实验室，当仁不让地选择了 VI。比较有意思的是，后续大多数 LDA 相关的论文都选择了 MCMC 为主的**吉布斯（Gibbs）**采样来作为学习算法。

VI 的完整讲解无法在本文涵盖。从最高的层次上来理解，VI 是选取一整组简单的、可以优化的所谓变分分布（Variational Distribution）来逼近整个模型的后验概率分布。当然，由于这组分布的选取，有可能会为模型带来不小的误差。不过好处则是这样就把贝叶斯推理的问题转化成了优化问题。

从 LDA 的角度来讲，就是要为θ以及 z 选取一组等价的分布，只不过更加简单，更不依赖其他的信息。在 VI 进行更新θ以及 z 的时候，算法可以根据当前的θ以及 z 的最新值，更新α的值（这里的讨论依照原始的 LDA 论文，忽略了β的信息）。整个流程俗称**变分最大期望（Variational EM）**算法。

文章在 TREC AP 的文档数据中做了实验。首先，作者们使用了一个叫困惑度（Perplexity）的评估值来衡量文档的建模有效程度，这个值越低越好。LDA 在好几个数据集中都明显好于 PLSI 以及其他更加简单的模型。从这篇文章之后，主题模型的发展和对比都离不开困惑度的比较，也算是开启了一个新时代。

然后，作者们展示了利用 LDA 来做文档分类，也就是利用文档主题向量来作为文档的特征，从而放入分类器中加以分类。作者们展示了 LDA 作为文档分类特征的有力证据，在数据比较少的情况下优于文本本身的特征。不过总体说来，在原始的 LDA 论文中，作者们并没有特别多地展现出 LDA 的所有可能性。

总结

本文梳理了 LDA 提出的背景以及这篇论文所引领的整个领域的情况。

需要掌握的核心要点：

第一，论文作者们目前的状态；

第二，LDA 模型本身和它的一些特点；

第三，LDA 的训练流程概况以及在原始文章中的实验结果。

百科介绍

百度百科（详情）

LDA（Latent Dirichlet Allocation）是一种文档主题生成模型，也称为一个三层贝叶斯概率模型，包含词、主题和文档三层结构。所谓生成模型，就是说，我们认为一篇文章的每个词都是通过“以一定概率选择了某个主题，并从这个主题中以一定概率选择某个词语”这样一个过程得到。文档到主题服从多项式分布，主题到词服从多项式分布。

LDA是一种非监督机器学习技术，可以用来识别大规模文档集（document collection）或语料库（corpus）中潜藏的主题信息。它采用了词袋（bag of words）的方法，这种方法将每一篇文档视为一个词频向量，从而将文本信息转化为了易于建模的数字信息。但是词袋方法没有考虑词与词之间的顺序，这简化了问题的复杂性，同时也为模型的改进提供了契机。每一篇文档代表了一些主题所构成的一个概率分布，而每一个主题又代表了很多单词所构成的一个概率分布。

维基百科（详情）

在自然语言处理中，潜在Dirichlet分配（LDA）是一种生成统计模型，它允许未观察到的组解释观察集，解释为什么数据的某些部分是相似的。例如，如果观察是收集到文档中的单词，则假定每个文档是少量主题的混合，并且每个单词的存在可归因于文档的主题之一。LDA是主题模型的示例。