线性判别分析 (LDA) 介绍

逻辑回归通常是处理两类分类问题的算法。然而，当我们面对多于两个类别的分类任务时，线性判别分析（Linear Discriminant Analysis, LDA）成为首选的线性分类方法。

LDA 的模型表示

LDA 的模型非常直观，它主要依赖于数据的统计特性来为每个类别建立描述。对于单一输入变量，LDA 涉及以下统计量：

• 每类的均值：计算每个类别中该特征的平均值。

• 全局方差：在所有类别中计算整个特征的方差。

注意: 上述内容是关于LDA的基本概念和它如何通过简单的统计属性来表征不同类别之间的差异。

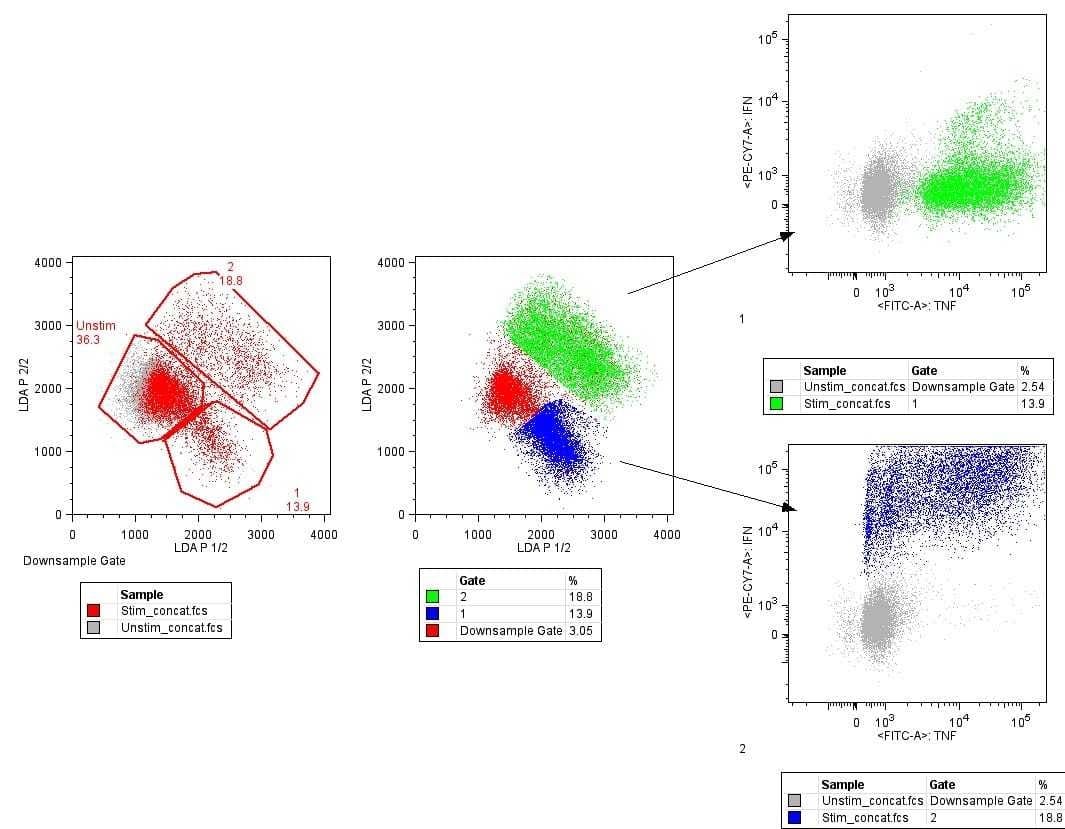
线性判别分析（LDA）是一种用于分类预测建模的技术，它通过计算每个类的判别值并选择具有最大值的类来进行预测。该方法假设数据遵循高斯分布（即钟形曲线），因此通常建议在应用LDA之前从数据中删除异常值。LDA因其简单性和有效性，在处理分类问题时非常有用。

百度百科（详情）

线性判别分析(linear discriminant analysis，LDA)是对费舍尔的线性鉴别方法的归纳，这种方法使用统计学，模式识别和机器学习方法，试图找到两类物体或事件的特征的一个线性组合，以能够特征化或区分它们。所得的组合可用来作为一个线性分类器，或者，更常见的是，为后续的分类做降维处理。

维基百科（详情）

线性判别分析（LDA），正态判别分析（NDA）或判别函数分析是Fisher线性判别式的推广，这是一种用于统计，模式识别和机器学习的方法，用于找出表征或分离两个或两个以上类别的特征的线性特征组合。得到的组合可以用作线性分类器，或者更常见地，用于在稍后分类之前降低维数。