融慧金科 AI Lab团队稿

1.背景介绍

书籍推荐

首先，想向各位读者推荐一本电子书籍《Interpretable Machine Learning》，其原因有两个：

1.该书作者从2017年首次在网络发布本书之后至今一直在持续更新，在github上可以看到其最新的更新时间是今年的6月30日。作者这样的科研精神，值得每一个相关从业者尊敬；

2.该书对机器学习模型可解释性进行了系统且有条理的总结，省去了读者查询文献的时间。通过阅读该书能够很快地对这一领域建立起一个基础的知识体系，同时也能给有应用需求的读者提供理论基础，本文内容在很大程度上也受益于这本电子书，非常适合对这一领域有进一步了解兴趣的读者阅读。

模型为什么需要解释？

此处想引用书中的一句话：

“If the user do not trust a model or a prediction,they will not use it.”

当我们在建立相关的模型过程中，我们需要验证模型的正确性与合理性。相比于客观的模型衡量标准如AUC、召回、准确率等，实际模型的使用人员更关心的是一些实际与业务相关的问题，如“模型做出这个决定依据是什么？”，“这个用户为什么会被拒绝？这个理由合理么？”。当建模人员得到在模型衡量标准上表现良好的模型，是否意味着在实际问题中表现良好呢？

书中作者给出了一个这样的例子，利用邮件文本内容判断是“无神论者”还是“基督徒”。在利用随机森林模型建立模型之后，模型在测试集上的准确率达到了92.4%。但是当利用模型解释器去探究模型分类的依据时发现，将邮件判断为“无神论者”的关键词汇是“Posting”,“Host”,“edu”一系列不被常识认可的词汇。这样的模型虽然在准确率上表现很好，但是其在之后的实际中能否满足模型需求，存在较大偏差。

在上述的案例中我们可以发现，对模型进行解释，能够帮助建模人员校验模型的有效性，从而保证模型的“线下”效果能够顺利迁移到“线上”。利用工具对模型进行解释，可以辅助建模人员或业务人员对模型结果有更加深入的理解，因此成为当下一个兼具应用价值与研究意义的课题。

2.模型解释常用分类方法

模型可解释性的常用方法，可以大致根据是否依赖被解释模型，以及模型解释的全局性进行分类。

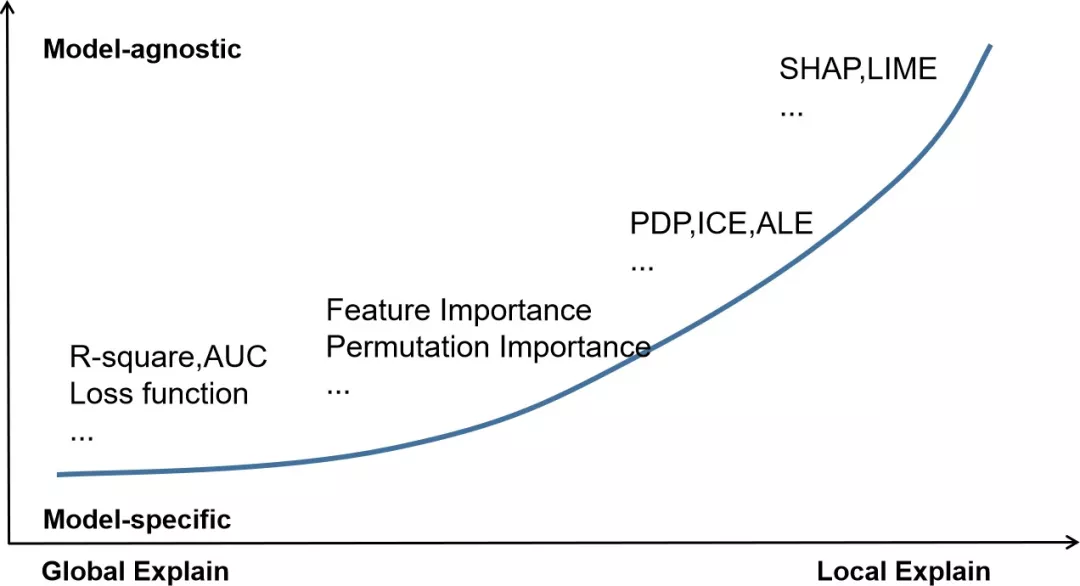
依赖模型或不依赖模型?

(Model-speciﬁc or model-agnostic)

根据解释方法对需要解释模型的依赖关系可以将模型解释方法分为： 依赖模型的解释方法与不依赖模型的解释方法。

依赖模型的解释方法，是指依据被解释模型自生的原理与结构，提取其结果或者中间过程作为对某一特征或者整个模型预测结果的解释。例如，线性模型中的p-value,R-square都是建立在被解释模型的假设条件下所建立的模型解释；XGBoost模型，可以使用在模型生成过程中特征的作为分裂依据的次数(freq)，影响观测结果的数量(cover)以及特征贡献的增益(gain)，作为对变量重要性的解释。

但是上述方法存在一些缺点：

1.基于不同模型的解释结果，之间往往不存在可比性。

2.解释结果需要使用者具备一定的模型理解与专业知识。

局部的或全局的？

(Local or global)

模型解释方法，根据模型的解释结果是针对整体模型的解释还是局部样本表现的可以分为：全局与局部的解释方法。

常见的全局解释通常是对整个模型的结果的解释，如特征重要性，模型结构(如树模型)。而局部的模型解释则是针对某一个实例的模型预测结果的解释，比如卡模型，单个实例各个变量取值得分。

不依赖模型的局部可读的模型解释方法

(Local Interpretable Model-Agnostic Explanations)

在融慧金科的实际应用场景中，需要对不同模型中各个中间产品结果进行解释（如人群画像，风险评价），并且希望这些解释的结果能够对实际的业务人员在生产过程中产生帮助（如风险审核人员）。因此，不依赖于模型本身的局部模型解释方法是我们的首要选择。

3. 基于边际效应的模型可解释性

部分依赖图

(Partial Dependence Plot)

部分依赖图（PDP）展示的是一个或者多个变量在全局角度上对模型输出结果的影响关系，是在待解释变量的变动引起模型变化的边际效应的期望，其公式如下所示：

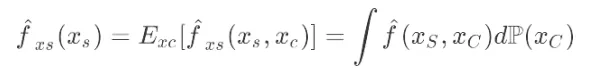
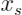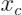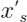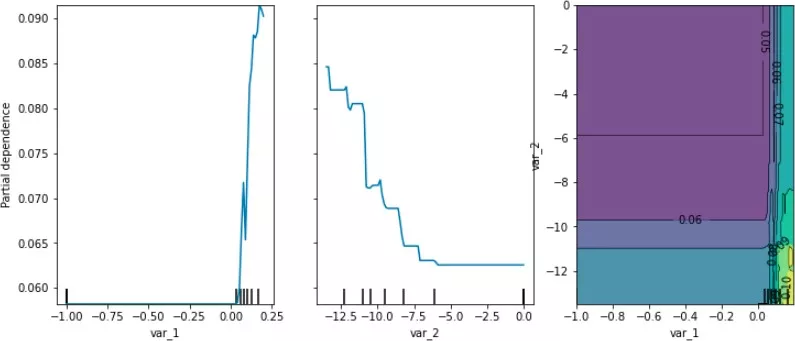
其中，是待解释的变量，是其余变量，PDP计算方法是对于一个固定取值在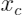所有可能性下的模型输出的均值。利用Sklearn中的PDP绘制效果如下：

个体期望条件图

(Individual Conditional Expectation)

个体期望条件（ICE）是在PDP图的基础上对模型中的样本进行抽样。其中，每一条曲线表示单独一个样本的待解释变量影响模型结果的边际效应的期望：

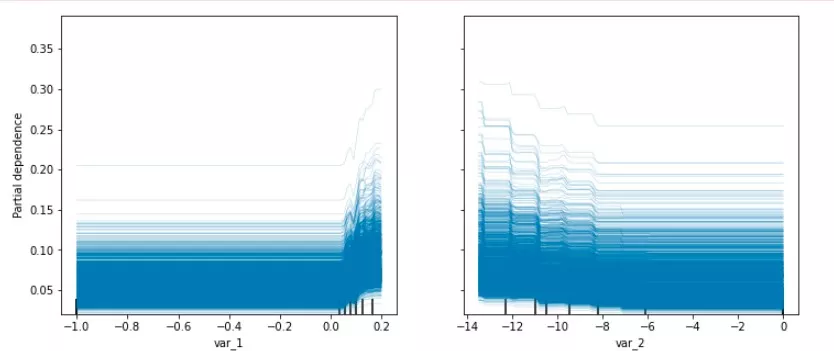
通过上述的PDP与ICE图可以看出：

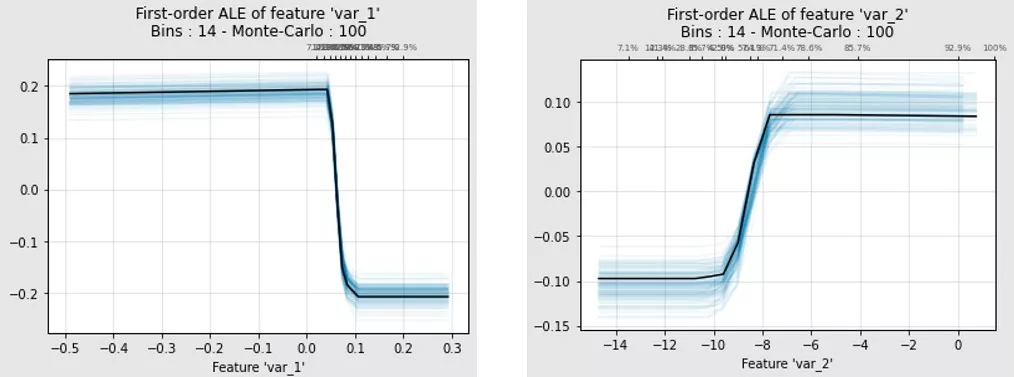
VAR_1特征取值在0以下，对模型取值结果影响不明显。当VAR_1超过0时，会使得模型结果明显上升，认为样本风险较高。VAR_2特征取值低于-0.5时，特征取值越低模型得分越高，大于-0.5时模型结果趋于平稳。通过两个特征的交互特征结果可以看到VAR_1取0以上，VAR_2取-12时模型分数取到最大，即样本风险最高。

累积局部效应法

(Accumulated Local Eﬀects,ALE)

然而，上述的PDP与ICE方法有一个重要的前提，待解释变量与其他变量之间相互独立。但是在风控场景中，很多情况下不能满足这样的假设。

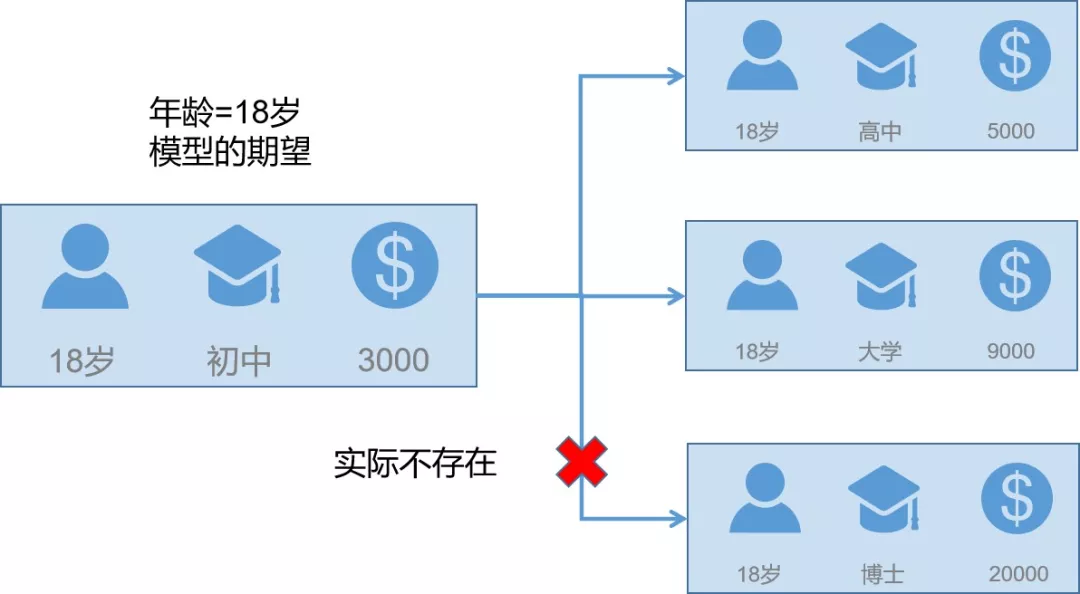
举一个例子： 针对人群的画像中通常都会有年龄与学历的画像内容，假设年龄被分为了{18以下，18-35，35-60，60以上}，学历被划分为{高中以下，高中，本科，硕士，博士及以上}。很明显正常的样本是不会出现{“年龄”:“18岁以下”,“学历”:“博士及以上”}表现的，但是PDP在计算边际效应时会考虑上述样本，并且与其他表现更为常见的情况权重相同，这就导致了解释结果上的偏差。解决上述问题，可以使用条件分布而非原本的边际效应：

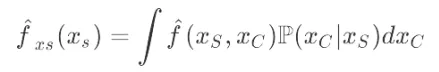
这种解释方法被称为累积局部效应法(Accumulated Local Eﬀects,ALE)，经过局部累计效应修正后解释结果如下：

4. 基于模型的可解释性工具

上述模型解释的方法，可以简单直观地描绘出特征变换带来的模型输出结果变化。如果需要更加详细的对模型中各个变量进行解释，则需要借助于一些简单的模型，其中 LIME 与 SHAP 应用较为广泛。

依赖于模型的解释方法的核心思想是，针对目标样本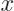选择其相邻样本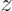，用一个简单且可读的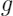模型拟合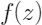做为模型的解释，转化为公式表示为：

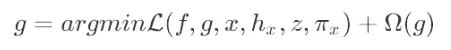
其中：

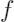是已经训练好的带解释模型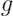，是一个简单模型用于解释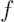，正则化项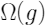限定了解释模型的复杂程度。

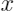是待解释的样本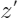，是用来辅助解释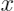所用的样本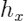，是生成特征取值的函数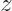，是选取样本的特征取值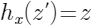，待解释样本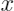与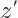之间的相关关系用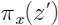表示。

进一步地将损失函数定义为 加权最小二乘 ，上述式子可以写为：

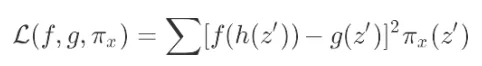
LIME

依照上述的式子，LIME的主要思想为：

随机选取离观测目标节点相邻的样本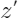，并随机扰乱其观测结果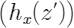生成新特征。
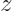选择线性回归作为解释模型，即: 。
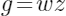衡量样本距离的权重:

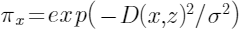（其中D(x,z)为距离衡量公式，如欧氏距离）

SHAP

SHAP的主要思想是Shapley Value，Shapley Value是一种来自博弈论的方法，用来告诉我们如何在各特征之间公平分配“收益”。SHAP则是将LIME与Shapley Value相结合：

随机选取待解释样本中的特征的候选集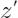，其中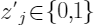表示该特征是否保持的原观测样本的特征。随机的将候选特征外的特征替换为全部样本中抽取的结果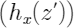，得到最终的特征。
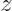同样选择线性回归作为解释模型：

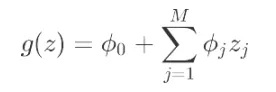
衡量样本距离的权重中表示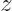的增长，即选取的样本于原样本一致的数量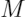，是可能选取特征候选数量：

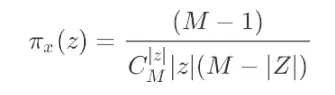
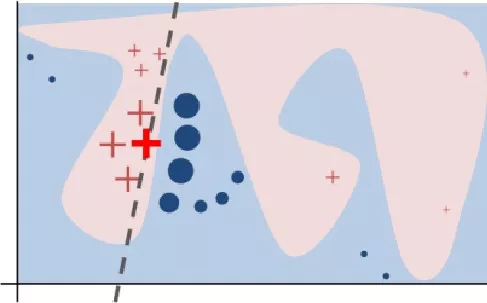
样本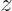的生成的一个例子如下图所示：

对于带观测样本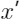其特征取值为{“Age”:0.5,“Weight”:20,“Color”:“Blue”}，随机生成一个候选特征向量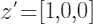。对于这样一个候选特征向量，将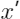中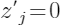位置上的特征随机的从所有样本中抽取一个作为替代，则产生了一个新的观测结果 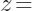{“Age”:0.5,“Weight”:17,“Color”:“Pink”}。

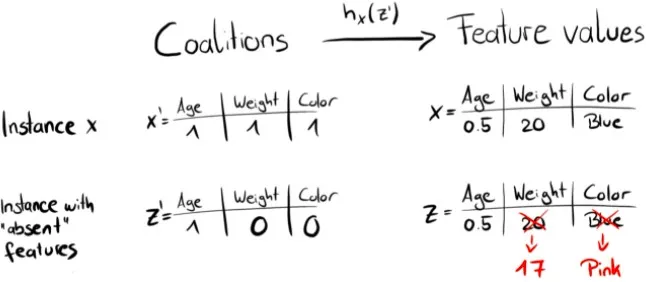
5. 融慧金科在模型可解释性的应用

模型可解释方法在实际建模过程中，能为建模人员带来多方面的帮助，接下来是两个示例：

5.1 反欺诈场景

该案例采用的是一个消费金融场景下的反欺诈模型，利用XGBoost进行训练。完成模型之后，希望对模型拒绝的用户给出其被拒绝的重要原因，并分析模型判读用户为高风险用户的主要依据：

1）变量重要性：

SHAP可以提供基于Shapley Value计算出的变量重要性，同时还能绘制出其取值分布与模型结果的关系，如下图所示：

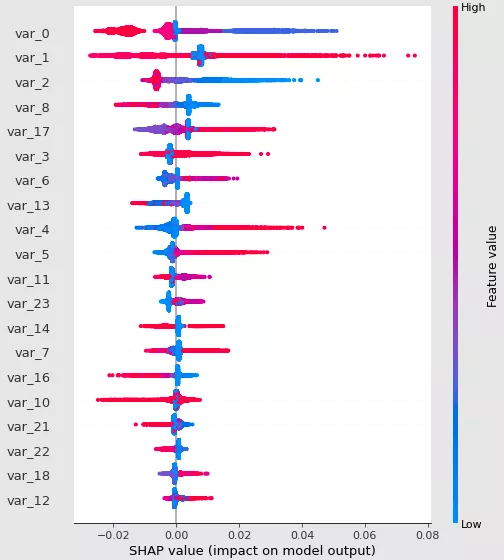
上图为summary_plot的结果，其中可以看出var_0,var_1,var_2对模型影响最强。同时上图也可以看出变量取值于模型结果的分布情况，其中变量var_1,var_2分布关系之前PDP绘制结果一致。

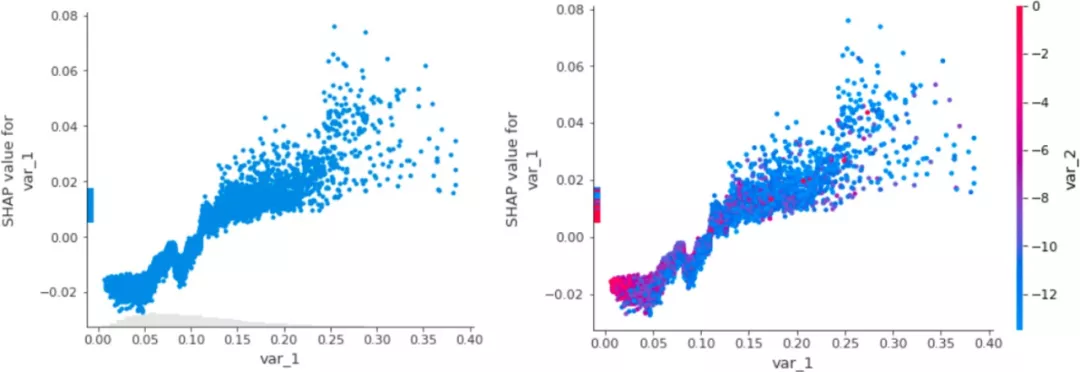
2）部分依赖关系：

依据SHAP的结果也可以绘出于PDP类似的部分依赖关系的散点图，对单变量与多变量交互结果进行分析，可以看出在单变量散点分布上，var_1取值的升高会使得模型总体评分上升，其中在var_1=0.1处还有一个明显折点，可以进一步分析。而两个变量交换的结果也可以发现，当var_1和var_2同时处于角度水平是模型平均结果较低，反之亦然。

3）单样本模型解释：

提取模型输出结果中风险最高的样本与查看其SHAP解释结果：

最高风险设备

可以看到被模型评判为最低风险的样本恰与最高风险样本相反：

①var_处于较低水平；

②var_0处于最高水平。

5.2 设备分类场景

这里展示的是一种模型可解释对模型效果验证的一种帮助。在风控场景中，很多情况需要对设备的用途与类型进行分类，比如需要判断这个设备是商用的还是家庭使用。然而这样的设备样本缺乏直接的标注结果，通常只能通过一些强规则或者历史累计的经验样本进行标注，才能进一步建立模型。因为数据的标注存在一定误差，所以在验证模型效果时，仅用离线的数据进行衡量可能出现较大误差。可以对模型的输出结果进行解释，查看其结果与常识或者假设是否一致：

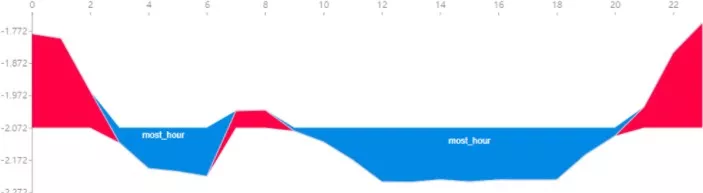
这里被解释的特征most_hour是设备上线的时间，我们可以发现设备最长使用时间在 晚上20点至次日8点 之间被判断为家庭使用设备，与我们常识认知有高度的一致性，可以一定程度上证明该模型的有效性，也可以直接通过模型解释的结果产生强规则用于生产过程。

6 . Conclusion

融慧金科在不断地尝试将上述模型可解释性方法应用到实际的生成过程中。模型解释工具不仅能够帮助业务人员更好地理解模型结果，同时能帮助算法人员对模型从有效性、合理性有一个新的认识，并帮助其对模型进行分析与矫正。甚至有些时候模型的解释结果可以直接作为一些关键性策略，从而直接对产品产生帮助。

之后，融慧金科将继续探索与尝试模型解释在各�

文章目录

金融场景下的模型可解释性应用探索