这次的系列文章将会介绍 NLP 领域语言模型及词向量表示的发展史，原理篇会从远古时代的 one-hot 出现讲到时代新星 bert 及其改进，同时后续的实践篇将会介绍预训练模型在房产领域的工业实践应用，带你填上一个个的大坑。话不多说，操练起来~

语言模型及词向量

何为语言模型？这是一个要贯穿整篇文章的问题。所谓语言模型，就是判断一句话是不是人话的模型，也就判断出是 P(the\ a\ zhou\ is\ a\ singer)> P(singer\ a\ zhou\ is\ jay) 的模型。当然，计算机并不认识周杰伦，它只知道 0 和 1，所以我们让模型进行判断时，需要将丰富的文字转换成冷冰冰的数字，这样计算机才能帮助我们进行计算，这也就是词向量的由来和存在的意义。

一个好的语言模型就是判断一句人话的概率尽可能的高，判断非人话的概率尽可能的低。那什么是一个好的词向量呢？举个例子，比如当我们人类看到‘woman’和‘female’时，会觉得这两个词应该是相似的意思，那么一个好的词向量表示就是让计算机通过计算这两个词向量，得出这两个词相似的结论。一般就是让计算机通过计算两个向量之间的距离来进行判断。所以如何让计算机看到的词向量和我们看到的词具有相同的意义，这是研究词向量的究极目标。

语言模型往往需要借助词向量进行计算，一个好的语言模型的诞生往往会伴随着质量较高的词向量的出现，因此词向量往往是语言模型的副产品。当然，优秀的事务往往不是一蹴而就的，语言模型和词向量的发展也经历了多个阶段。从词向量的角度来简单分类的话，大致可以分为 one-hot 表示和分布式表示两个大阶段，下面将从这个角度进行介绍。

一、one-hot 表示

one-hot 的想法简单粗暴，目的单纯，在我们的大脑和计算机之间架起了第一道桥梁。one-hot 将每一个词表示成一个固定维度的向量，维度大小是词表大小，向量中单词所在位置为 1，其他位置为 0。举个栗子，假设我们的词库里只有如下 7 个词

my,on,the,bank,river,woman,female

那么 bank 这个单词就可以表示为[0,0.0,1,0,0,0]，on 可以表示为[0,1,0,0,0,0,0]，以此类推。

但是想法过于简单总是会出问题的，one-hot 存在的两个明显问题： 维度灾难 和 语义鸿沟。

所谓维度灾难就是 one-hot 的向量维度是和词库大小一致的，一般我们的词库会很大，比如当我们的词库里有 100000 个词，那么一个词向量的维度就是 1 * 100000，这就导致 one-hot 表征的向量维度很大，使得数据样本稀疏，距离计算困难，造成维度灾难。当维度灾难发生时，一个样本的特征就会过于多，导致模型学习过程中极其容易发生过拟合。

所谓语义鸿沟的问题是因为 one-hot 生成的词向量都是彼此正交的，体现不出任何语义上的联系。比如 on 表示为[0,1,0,0,0,0,0]，woman 表示为[0,0.0,0,0,1,0]，female 表示为[0,0.0,0,0,0,1]，on 和 woman 这两个向量相乘结果是 0，female 和 woman 这两个向量相乘也是 0，所以无法表现出 on 和 woman 不相似，female 和 woman 相似这种语义上的联系。

二、分布式表示

鉴于 one-hot 表示的缺点，我们希望能有低维稠密的词向量出现，同时这些向量之间能够存在语义上的联系，所以分布式表示就带着历史使命出现了。分布式表示描述的是将文本分散嵌入到另一个空间，一般是将高维映射到低维稠密的向量空间。分布式表示依据的理论是 Harris 在 1954 年提出的分布式假说，即： 上下文相似的词，其语义也相似。

2.1 基于 SVD

这一类方法的一般操作是将共现矩阵 A 进行 SVD 分解，即 A=U\Sigma V^T，，然后取分解后的 U 的作为词向量矩阵（一般取 U 的子矩阵）。所以啥是共现矩阵，啥是 SVD 呢？

2.1.1 共现矩阵

共现矩阵一般有两种，第一种叫 Window based Co-occurrence Matrix，是通过统计指定窗口大小的单词共现次数构成的矩阵，举个栗子，假设我们的语料库中只有三个句子

I like deep learning.
I like NLP.
I enjoy flying.

选取窗口大小为 3，那么构成的共现矩阵 A 如下图所示

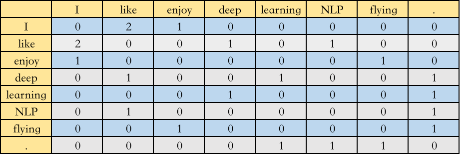
第二种叫 Word-Document Matrix，是将单词在文档中出现的频率构成矩阵，再举个栗子，假设我们一共有三篇文档

document1: I like deep learning. I enjoy deep learning
document2: I like NLP.
document3: I enjoy flying.

那么构成的共现矩阵 A 如下图所示

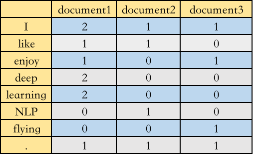
2.1.2 SVD

前面提到，SVD 是将矩阵 A 进行分解，A=U\Sigma V^T，其中 A 是 m*n 的矩阵，U

是 m*n 的矩阵，\Sigma 是 m*n 的矩阵，V 是 n*n 的矩阵，如何求解得到这三个矩阵呢？

首先回顾一下特征值和特征向量的定义：

Ax=\lambda_x

其中，A 是 m*m 实对称矩阵，x 是一个 n 维向量，则称 \lambda 是一个特征值，x 是矩阵 A 的特征值 \lambda 对应的一个特征向量。如果我们求出了 n 个特征值 \lambda_1, \lambda_2…\lambda_n 及其对应的特征向量 x_1,x_2…x_n，如果这 n 个特征向量线性无关，那么矩阵 A 就可以表示为

A=X\Sigma X^{-1}

其中，X 是有 n 个特征向量组成的 n*n 的矩阵，\Sigma 是由 n 个特征值为主对角线的 n*n 维矩阵。一般会将 X 进行标准化，即 ||x_i||_2=1,x_ix^T_i=1,XX^T=I，也就是得到了 X^T=X^{-1}，那么 A 就可以表示为

A=X\Sigma X^T

需要注意的是，直接进行特征分解的矩阵 A 是方阵，而在 SVD 中的矩阵 A 不一定是方阵，这时需要再做一些推导。

AA^T=U\Sigma V^TV \Sigma^T U^T

由于 V^TV=I，所以

AA^T=U\Sigma^2U^T

因为 AA^T 是一个 m*m 的方阵，所以通过求解 AA^T 的特征向量，就可以得到矩阵 U。同理，通过求解 A^TA 的特征向量，就可以得到矩阵 V，通过对 AA^T 的特征值矩阵求平方根，就可以得到矩阵 A 的奇异值矩阵 \Sigma。至此，我们得到了矩阵 A 的分解。

值得注意的是，奇异值是从大到小排列的，通常前 10% 甚至 1% 的奇异值的和就占了所有奇异值和的 99% 以上，奇异值在集合意义上代表了特征的权重，所以我们一般不会选择将整个 U 矩阵作为词向量矩阵，而是选择前 k 维，最终的词向量表大小就是 m*k ,m 是词表达小，k 是词向量维度。

基于 SVD 的方法得到了稠密的词向量，相比于之前的 one-hot 有了一定提升，能够表现单词之间一定的语义关系，但是这种方法也存在很多问题：

  • 矩阵过于稀疏。因为在构建共现矩阵时，必然有很多词是没有共现的

  • 分解共现矩阵的复杂度很高

  • 高频无意义的词影响共现矩阵分解的效果，如 is，a

  • 一词多义问题，即同一个词具有不同含义却被表示为一个向量，比如 bank 既有银行的意思，也有岸边的意思，但在这里被表示为统一的向量

2.2 基于语言模型

基于语言模型的方法抛弃了共现矩阵这种问题重重的东西，转而通过构建语言模型来产生词向量。so，啥是语言模型呢？

标准定义：对于语言序列 w_1, w_2, …,w_n,，语言模型就是计算该序列出现的概率，即 P(w_1, w_2,…,w_n)

通俗理解：构建一个模型，使得看起来像人话的句子序列出现的概率大，非人话的句子序列出现的概率小，也就是 code

语言模型一般包括统计语言模型和神经网络语言模型，统计语言模型一般就是指 N-gram 语言模型，神经网络语言模型包括 NNLM、Word2vec 等。

2.2.1 N-gram

N-gram 就是一个语言模型，其目的并非产生词向量，一般用于判断语句是否合理或者搜索 sug 推荐，这里简单一提。

前面说了，语言模型计算一句人话的概率，也就 P(w_1, w_2,…,w_n)，利用链式法则可知

P(w_1,w_2,…,w_n)=P(w_1)P(w_2|w_1)P(w_3|w_1,w_2)…P(w_n|w_1,w_2,…w_n) \\ =P(w_1)P(w_2|w_1)P(w_3|w_1^2)…P(w_n|w_1^n)

直接计算上式计算量太大，所以 N-gram 模型引入马尔科夫假设，即当前词出现的概率只与其前 n-1 个词有关

P(w_i|w^{i-1}_1)\approx P(w_i|w^{i-1}_{i-n+1})

当语料足够大时

P(w_i|w^{i-1}_{i-n+1}) \approx \frac {Count(P(w^i_{i-n+1}))}{Count(P(w^{i-1}_{i-n+1}))}

真正常用的 N-gram 的 n 不会超过 3，一般为 n=2。当 n=2 时，利用上式计算一句话的概率

P(w_1,w_2,…,w_n)=P(w_1|start)P(w_2|w_1)P(w_3|w_2)…P(w_n|w_{n-1})

2.2.2 NNLM

使用语言模型产生词向量的一个里程碑论文是 Bengio 在 2003 年提出的 NNLM，该模型通过使用神经网络训练得到了一个语言模型，同时产生了副产品词向量。模型的总体架构如下图所示，表达的思想是利用前 n-1 个词去预测第 n 个词的概率，所以这里的输入是 n-1 个词，输出是一个维度为词表大小的向量，代表每个词出现的概率。

NNLM 原理结构图：

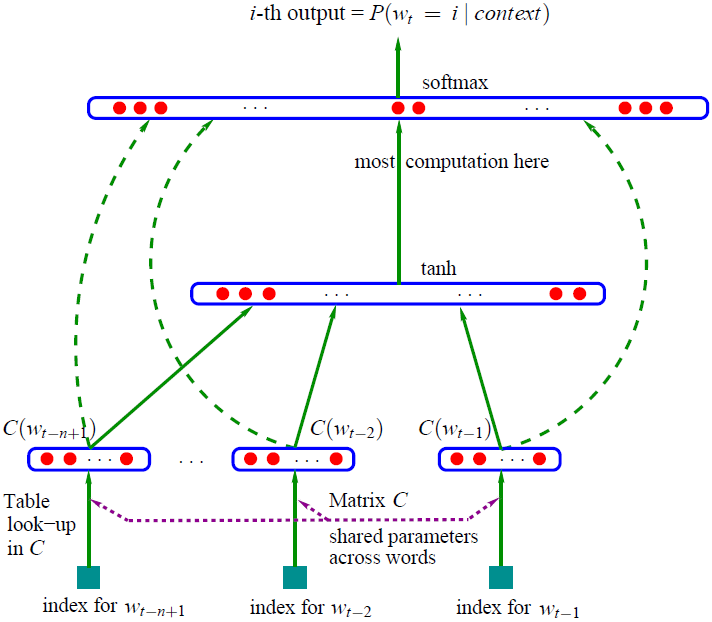
这个结构在现在看起来是很简单

  • 首先输入层将当前词 w_i 的前 n-1 个词 \{w_{i-n+1},…,w_{i-2},w_{i-1}\} 作为上文，通过对词向量表 C 进行 look-up 得到词向量表示 \{C_{i-n+1},…,C_{i-2},C_{i-1}\}，每个词的维度是 m*1

  • 然后将这 n-1 个词向量进行拼接，得到一个维度是 m(n-1)*1 的长向量 x，然后经过隐层计算，得到一个 |V|*1 的向量 y，模型训练过程中 最大的运算量 就在这一层

    y=b+w_x+Utanh(d+Hx)

参数 \Theta={b,d,W,U,H,C},，其中 b 和 d 是偏置，W \in R^{|V|*m(n-1)},U \in R^{|V|*h},H \in R^{h*m(n-1)} 是参数矩阵，W 是将词向量直连到输出时的参数，可以置为 0，m,n,h 是超参数。

利用 softmax 对输出概率进行归一化

\hat{P}(w_i|w^{i-1}_{i-n+1})= \frac {e^{y_{w_i}}}{\sum_j y_{w_j}}

  • 使用 交叉熵 作为损失函数，所以对于单个样本，其优化目标是就是 最大化，利用随机梯度下降进行优化 log\hat{P}(w_i|w^{i-1}_{i-n+1}) ，利用随机梯度下降进行优化

\Theta \leftarrow \Theta+\epsilon \frac{\partial log{\hat{P}(w_i|w_{i-n+1}^{i-1})}}{\partial \Theta}

优化结束后，得到了一个语言模型，同时得到了词向量矩阵 C。

NNLM 模型在获取词向量上的工作是奠基性的，但是其模型训练的复杂度还是过高，后续很多算法都是在 NNLM 的基础上进行改进，比如耳熟能详的 Word2vec 对其训练的复杂度进行了针对性的改进。

前面所讲的都是一些开胃小菜，建立该系列文章的核心概念–词向量。接下来我们将会对经典算法 Word2vec 单独拿出来进行详细的原理介绍~

三、word2vec

Word2vec 是谷歌团队在 2013 年开源推出的一个专门用于获取词向量的工具包，其核心算法是对 NNLM 运算量最大的那部分进行了效率上的改进，让我们来一探究竟。

3.1 Word2vec 原理解析

word2vec 有两种模型–CBOW 和 Skip-gram，这两个模型目的都是通过训练语言模型任务，得到词向量。CBOW 的语言模型任务是给定上下文预测当前词，Skip-gram 的语言模型任务是根据当前词预测其上下文。

Word2vec 还提供了两种框架–Hierarchical Softmax 和 Negative-Sampling，所以 word2vec 有四种实现方式，下面将对其原理进行介绍。

3.1.1 CBOW

3.1.1.1 结构

CBOW 的核心思想就是利用给定上下文 w_{t-2},w_{t-1},w_{t+1},w_{t+2} 预测当前词 w_t，其结构表示为

CBOW 结构：

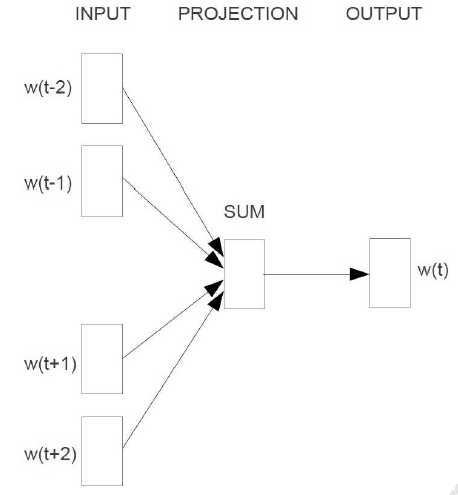
我们知道基于神经网络的语言模型的目标函数通常是对数似然函数，这里 CBOW 的目标函数应该就是

L=\sum_{w \in C} logP(w|Context(W) )

其中 Context(W) 是单词 w 的上下文，C 是词典。所以我们关注的重点应该就是 P(w|Context(W) 的构造上，NNLM 和 Word2vec 的本质区别也是在于该条件概率函数的构造方式不同。

构造方式不同。

3.1.1.2 原理

3.1.1.2.1 基于 Hierarchical Softmax

CBOW 模型的训练任务是在给定上下文 w_{t-2},w_{t-1},w_{t+1},w_{t+2}，预测当前词 w_t。基于 Hierarchical Softmax 的 CBOW 结构相当于在 NNLM 上的改进，如下图所示

基于 Hierarchical Softmax 的 CBOW 模型：

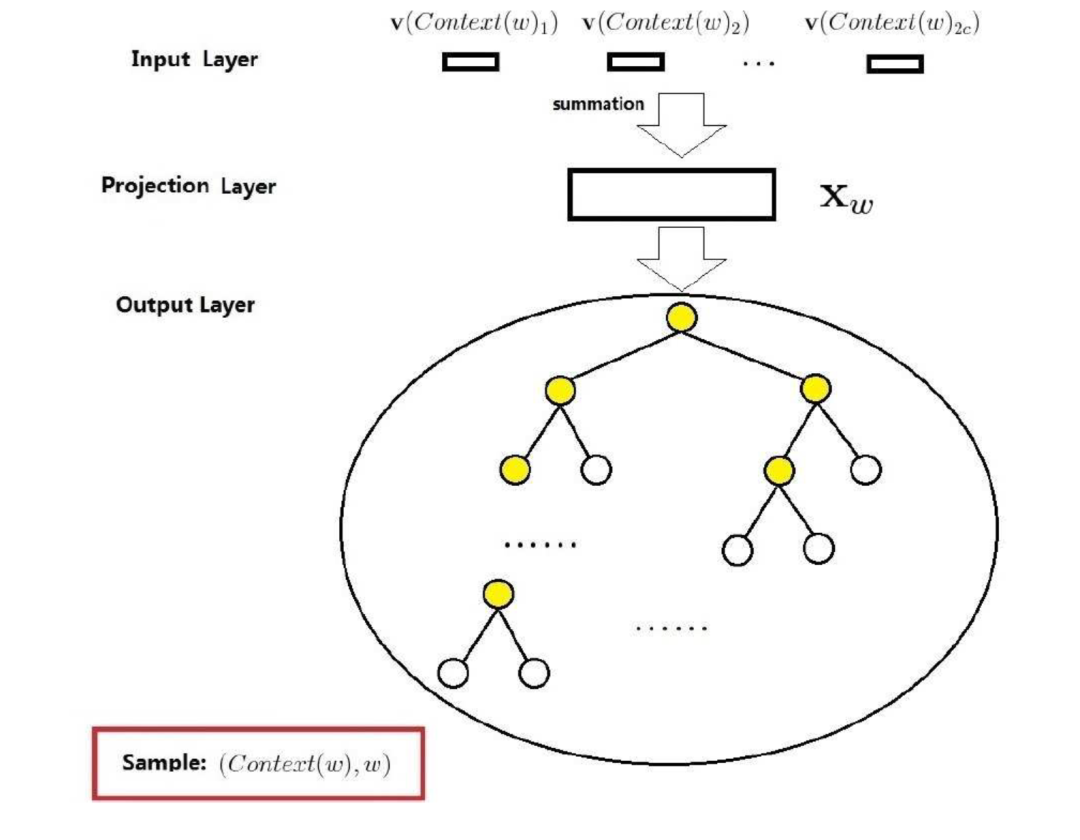
CBOW 模型一共是有三层，分别是输入层（input layer），投影层（projection layer）和输出层（output layer）。

输入层：输入是当前词的上下文，共 $2c$ 个词向量

投影层：投影层将 2c 个词向量进行累加，得到 X_w，即 X_w=\sum^{2c}_{i=1}v(Context(W) _i)，这里不包含当前词的向量表示

输出层：输出是一个用语料中出现的词为叶子结点构建的 Huffman 树，结点的权值是各词在语料中出现的次数。图中的 Huffman 树共 N 个结点，对应语料中的 N 个词，非叶子结点 N-1 个，即图中标黄的。

基于 Hierarchical Softmax 的 CBOW 模型和之前介绍的 NNLM 的主要区别：

  • 从输入层到投影层，CBOW 采用的是求和，而 NNLM 是拼接
  • CBOW 没有隐藏层
  • 输出层，基于 Hierarchical Softmax 的 CBOW 是树形结构，NNLM 是线性结构

之前说过，NNLM 的主要运算量就是在于隐藏层和输出层的 softmax 的计算量，基于 Hierarchical Softmax 的方法通过对这些关键点进行了针对性的优化，去掉了隐藏层，更改了输出结构，大大提升了运算效率。下面介绍基于 Hierarchical Softmax 的 CBOW 是如何利用树结构训练得到词向量的。

对于 huffman 的某个叶子结点，假设该结点对应词典 D 中的词 w，定义以下符号

  • p^w：从根结点出发到达 w 对应的叶子结点的路径
  • l^w：路径 p^w 中包含的结点个数
  • p^w_1,p^w_2,…,p^w_{l^w}：路径 p^w 中的 l^w 个结点，其中 p^w_1 代表根结点，代表词对应的结点
  • d^w_1,d^w_2,…,d^w_2 \in \{0,1\}：词 w 的 Huffman 编码，由 l^w-1 位编码构成，即根结点不对应编码
  • \Theta^w_1, \Theta^w_1,…,\Theta^w_1 \in R^m：路径 p^w 中非叶子结点对应的向量，\Theta^w_j 代表路径 p^w 中第 j 个非叶子结点对应的向量

下面通过一个示例说明运算原理，如下图所示，考虑当前词 w=“足球”，那么图中的红色边串起来的 5 个结点就构成路径 p^w，其长度 l^w=5，p^w_1,p^w_2,p^w_3,p^w_4,p^w_5 是路径 p^w 的 5 个结点，其中 p^w_1 对应的是根结点，d^w_2,d^w_3,d^w_4,d^w_5 分别是 1，0，0，1，即当前词“足球”的 Huffman 编码为 1001，\Theta^w_1, \Theta^w_2,\Theta^w_3,\Theta^w_4 分别是路径 p^w 上 4 个非叶子结点对应的向量。

CBOW 原理示例：

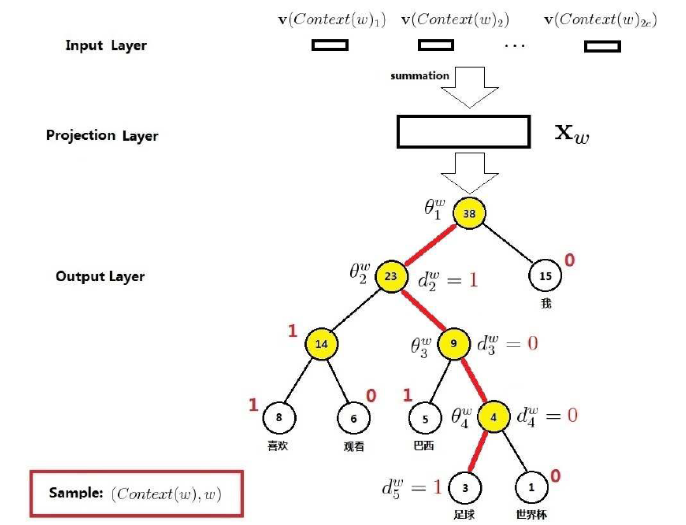
所以，讲了这么多，我们的重点 p(w|Context(W) ) 究竟是怎么构建的呢？

我们知道词库里的每一个词都可以被表示为一个 Huffman 编码，如果把 Huffman 树每一个结点都看成一次二分类，那么这个语言模型的任务就变成输入上下文，使得当前词的 Huffman 编码对应的路径的概率最大。这里约定将一个结点进行二分类时，分到左边为负类，分到右边为正类（主要为了和源码对应），即

label(p^w_i)=1-d^w_i,i=2,3,…l^w

由前面介绍的逻辑回归可以知道，结点分为正类的概率是

\sigma(X_w^T\Theta)=\frac{1}{1+e^{-X_w^T\Theta}}

所以分为负类的概率就是 1-\theta(X^T_w\Theta ) 。这里的 X_w 就是当前词 w 的上下文通过求和得到的，\Theta 就是每一个结点的 \Theta^w_i，是待训练参数。

举个栗子，还是前面说的当前词是“足球”，从根结点出发到达这个词一共需要经过 4 次二分类

  • 第一次：p(d^w_2|X_w,\Theta^w_1)=1- \sigma(X^T_w\Theta^w_1)
  • 第二次：p(d^w_3|X_w,\Theta^w_2)=\sigma(X^T_w\Theta^w_2)
  • 第三次：p(d^w_4|X_w,\Theta^w_3)=\sigma(X^T_w\Theta^w_3)
  • 第四次：p(d^w_5|X_w,\Theta^w_4)=1- \sigma(X^T_w\Theta^w_4)

所以对于当前词“足球”，我们的条件概率函数为

p(足球 |Context(足球))=\prod_{j=1}^5 p(d^w_j|X_w,\Theta^w_{j-1})

由上面的小例子，我们可以扩展出一般的条件概率公式

p(w|Context(W) )=\prod_{j=2}^{l^w} p(d^w_j|X_w,\Theta^w_{j-1})

其中

p(d^w_j|X_w,\Theta^w_{j-1})=\begin{cases}\sigma(x^T_w\Theta^w_{j-1}), d^w_j=0 \\1-\sigma(x^T_w\Theta^w_{j-1}), d^w_j=1 \\\end{cases}

写成整体表达式

p(d^w_j|X_w,\Theta^w_{j-1})=[\sigma(x^T_w\Theta^w_{j-1})]^{1-d^w_j}*[1-\sigma(x^T_w\Theta^w_{j-1})]^{d^w_j}

所以我们要优化的目标函数就是

L =\sum _{w \in C}logp(w|Context(W) ) \\ =\sum_{w \in C}log\prod_{j=2}^{l^w}p(d_j^w|X_w,\Theta_{j-1}^W) \\ =\sum _{w \in C}log\prod_{j=2}^{l^w}\{[\sigma(X_w^T\Theta _{j-1}^W) ]^{1-d_j^w} \cdot [1-\sigma(X_w^T\Theta _{j-1}^W) ]^{d_j^w}\} \\ = \sum _{w \in C}\sum_{j=2}^{l^w}log \{[\sigma(X_w^T\Theta _{j-1}^W) ]^{1-d_j^w} \cdot [1-\sigma(X_w^T\Theta _{j-1}^W) ]^{d_j^w}\} \\ = \sum _{w \in C}\sum_{j=2}^{l^w}\{log [\sigma(X_w^T\Theta _{j-1}^W) ]^{1-d_j^w} +log[1-\sigma(X_w^T\Theta _{j-1}^W) ]^{d_j^w}\} \\ =\sum _{w \in C}\sum_{j=2}^{l^w}\{(1-d_j^W) \cdot log [\sigma(X_w^T\Theta _{j-1}^W) ] +d_j^w \cdot log[1-\sigma(X_w^T\Theta _{j-1}^W) ]\}

令

L(w,j)=(1-d^w_j)*log[\sigma(x^T_w\Theta^w_{j-1})]+d^w_j*log[1-\sigma(x^T_w\Theta^w_{j-1})]

使用随机梯度上升法进行目标函数优化，下面推导一下梯度的计算

\frac {\partial L(w,j)}{\partial \Theta_{j-1}^w}=\frac{\partial}{\partial \Theta_{j-1}^w}\{(1-d_j^W) \cdot log [\sigma(X_w^T\Theta _{j-1}^W) ] +d_j^w \cdot log[1-\sigma(X_w^T\Theta _{j-1}^W) ]\} \\ =(1-d_j^W) [1-\sigma(X_w^T\Theta _{j-1}^W) ]X_w-d_j^w\sigma(X_w^T\Theta _{j-1}^W) X_w \\ = [1-d_j^w-\sigma(X_w^T\Theta _{j-1}^W) ]X_w

所以，更新参数 \Theta^w_{j-1} 时

\Theta_{j-1}^w:=\Theta_{j-1}^w+\eta [1-d_j^w-\sigma(X_w^T\Theta _{j-1}^W) ]X_w

其中，\eta 是学习率。

同理可以计算得到

\frac {\partial L(w,j)}{\partial X_w}=[1-d_j^w-\sigma(X_w^T\Theta_{j-1}^W) ]\Theta_{j-1}^w

我们最终想优化的向量是词表中的每一个词向量，而 X_w 是当前词上下文的累加，那么该如何更新每个词的向量表示呢？word2vec 中的做法很简单直接，就是将 X_w 的梯度变化等效于每个词的梯度变化，即

v(\tilde{w})=v(\tilde{w})+\eta\sum_{j=2}^{l^w}\frac {\partial L(w,j)}{\partial X_w},\tilde{w} \in Context(W)

至此，基于 Hierarchical Softmax 的 CBOW 模型的原理就介绍完了，通过不断训练就可以得到我们想要的词向量表。

3.1.1.2.2 基于 Negative-Sampling

基于 Negative-Sampling（负采样，NEG）的方法的目的是进一步提升训练速度，同时改善词向量的质量。NEG 不再使用相对复杂的 huffman 树，而是使用简单的随机负采样，大幅度提升性能。

CBOW 是利用上下文预测当前词，那么将当前词替换为其他词时，就构成了一个负样本。

书面一点，对于给定的 Context(W) ，词 w 就是一个正样本，其他词就是负样本，假设我们通过负采样方法选取好一个关于 w 的负样本子集 NEG(W) 。得到样本集后，我们的目标是最大化

G=\prod_{w \in C}g(W)

g(W) =\prod_{u \in \{w\}\bigcup NEG(W) }p(u|Context(W) )

其中

p(u|Context(W) )=\begin {cases}\sigma(X_w^T\Theta^u), &u=w \\ 1-\sigma(X_w^T\Theta^u), &u \neq w \end{cases}

所以

g(W) =\sigma(X_w^T\Theta^W) \prod_{u \in NEG(W) }[1-\sigma(X_w^T\Theta^u)]

这里，X^T_w 还是代表上下文 Context(W) 的词向量之和，\Theta^u 表示词 u 对应的一个待训练辅助向量。直观上看，这就是最大化 \sigma(X^T_w\Theta^W) 的同时，最小化 \sigma(X^T_w\Theta^u)，其中 u \in NEG(W) ，也就是最大化正样本的概率的同时最小化负样本的概率。

对于给定的语料库 C，最终的目标函数是

L= log\prod_{w \in C}g(W) =\sum_{w \in C }logg(W) \\ =\sum_{w \in C}log\{\sigma(X_w^T\Theta^W) \prod_{u \in NEG(W) }[1-\sigma(X_W^T\Theta^u)]\} \\ =\sum _{w \in C}\{log[\sigma(X_W^T\Theta^W) ]+\sum_{u \in NEG(W) }log[1-\sigma(X_W^T\Theta^u)]\} \=\sum _{w \in C}\{log[\sigma(X_W^T\Theta^W) ]+\sum_{u \in NEG(W) }log[\sigma(-X_W^T\Theta^u)]\}

为了推导梯度更新的过程，令

L(w,u)=\begin{cases}log[\sigma(x^T_w\Theta^u_{j-1})], u= w \\log[1-\sigma(x^T_w\Theta^u_{j-1})], u \neq w \\\end{cases}

所以

\frac{\partial L(w,u)}{\partial \Theta^u}=\begin{cases}(1-\sigma(X_w^T\Theta^u))X_w, &u=w \\ -\sigma(X_w^T\Theta^u)X_w,&u\neq w \end{cases}

\Theta^u:=\Theta^u+\eta \frac{\partial L(w,u)}{\partial \Theta^u}

同理：

\frac{\partial L(w,u)}{\partial X_w}=\begin{cases}(1-\sigma(X_w^T\Theta^u))\Theta ^u, &u=w \\ -\sigma(X_w^T\Theta^u)\Theta ^u,&u\neq w \end{cases}

v(\tilde{w}):=v(\tilde{w})+\eta \sum_{u \in \{w\} \bigcup NEG(W) } \frac{\partial L(w,u)}{\partial X_w} ,\tilde{w} \in Context(W)

3.1.2 Skip-gram

3.1.2.1 结构

Skip-gram 的核心思想就是利用给定的当前词 w_t，预测上下文 w_{t-2},w_{t-1}, w_{t+1}, w_{t+2}，其结构表示为

Skip-gram 结构：

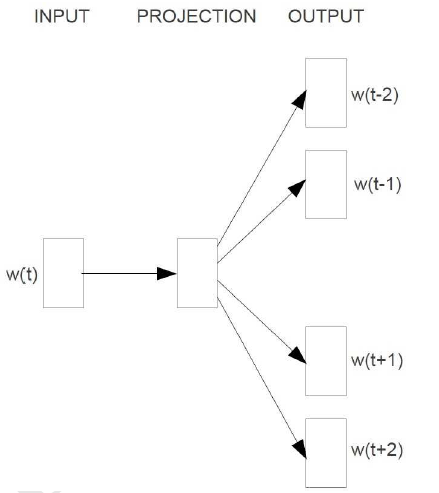
我们知道基于神经网络的语言模型的目标函数通常是对数似然函数，这里 Skip-gram 的目标函数应该就是

L=\sum_{w \in C}logp(Context(W) |W)

其中 Context(W) 是单词 w 的上下文，C 是词典。所以我们关注的重点应该就是 P(Context(W) |W) 的构造上。

3.1.2.2 原理

3.1.2.2.1 基于 Hierarchical Softmax

前面说了，Skip-gram 的语言模型任务是根据当前词预测其上下文，原理上和 CBOW 很相似，基于 Hierarchical Softmax 的 Skip-gram 的结构如下图所示

基于 Hierarchical Softmax 的 Skip-gram 模型：

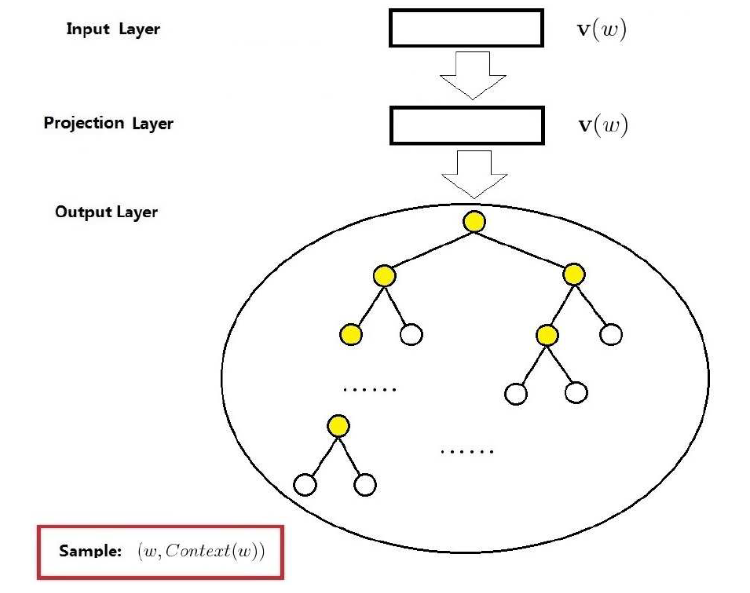
输入层：中心词 w 的词向量 v(W)

投影层：恒等投影，只是为了和 CBOW 模型进行对称类比

输出层：和 CBOW 一样，是一颗 huffman 树

Skip-gram 的重点是条件概率函数 p(Context(W) |W) 的构造，SKip-gram 中对于该条件概率函数的定义为

p(Context(W) |W) =\prod_{u \in Context(W) }p(u|W) \\ =\prod_{u \in Context(W) }\prod_{j=2}^{l^u}p(d_j^u|v(W) ,\Theta_{j-1}^u) \=\prod_{u \in Context(W) }\prod_{j=2}^{l^u}\{[\sigma(v(W) ^T\Theta_{j-1}^u)^{1-d_j^w} \cdot [1-\sigma(v(W) ^T\Theta_{j-1}^u]^{d_j^w}]\}

所以，Skip-gram 的目标函数为

L=\sum_{w \in C}logp(Context(W) |W) \=\sum_{w \in C}log\prod_{u \in Context(W) }\prod_{j=2}^{l^u}\{[\sigma(v(W) ^T\Theta_{j-1}^u)^{1-d_j^w} \cdot [1-\sigma(v(W) ^T\Theta_{j-1}^u]^{d_j^w}]\} \\ =\sum_{w \in C}\sum_{u \in Context(W) }\sum_{j=2}^{l^u}\{(1-d_j^W) \cdot log[\sigma(v(W) ^T\Theta_{j-1}^u]+d_j^u \cdot log[1-\sigma(v(W) ^T\Theta_{j-1}^u)]\}

令

L(w,u,j)=(1-d_j^W) \cdot log[\sigma(v(W) ^T\Theta_{j-1}^u]+d_j^u \cdot log[1-\sigma(v(W) ^T\Theta_{j-1}^u)]

则

\frac{\partial L(w,u,j)}{\partial \Theta_{j-1}^u}=\frac{\partial}{\partial \Theta_{j-1}^u}(1-d_j^W) \cdot log[\sigma(v(W) ^T\Theta_{j-1}^u]+d_j^u \cdot log[1-\sigma(v(W) ^T\Theta_{j-1}^u)] \=(1-d_j^W) [1-\sigma(v(W) ^T\Theta_{j-1}^u)]v(W) -d_j^u\sigma(v(W) ^T\Theta_{j-1}^u)v(W) \=[1-d_j^u-\sigma(v(W) ^T\Theta_{j-1}^u)]v(W)

所以

\Theta_{j-1}^u:=\Theta_{j-1}^u+\eta [1-d_j^u-\sigma(v(W) ^T\Theta_{j-1}^u)]v(W)

同理

\frac{\partial L(w,u,j)}{\partial {v(W) }}=[1-d_j^u-\sigma(v(W) ^T\Theta_{j-1}^u)]\theta_{j-1}^u

v(W) :=v(W) +\eta \sum_{u\in Context(W) } \sum_{j=2}^{l^u}\frac{\partial L(w,u,j)}{\partial v(W) }

3.1.2.2.2 基于 Negative-Sampling

基于负采样的 skip-gram 模型基本与前面基于负采样的 CBOW 推导的类似，目标函数为

G=\prod_{w \in C}\prod _{u \in Context(W) }g(u)

也就是当给定当前词 w 时，希望其上下文 Context(W) 出现的概率最大，其中

g(u)=\prod _{z \in \{u\} \bigcup NEG(u)}p(z|W)

p(z|W) =\begin {cases} \sigma(v(W) ^T\Theta ^z), & z=u \\ 1-\sigma(v(W) ^T\Theta ^z),&z\neq u\end{cases}

这里 g(u) 代表的就是上下文 Context(W) 中某个词出现的概率，NEG(u) 表示处理词 u 时生成的负样本子集，v(W) 是输入的当前词，\Theta^z 是待训练的辅助向量。

所以

L =logG=log\prod_{w \in C}\prod _{u \in Context(W) }g(u) \\ =\sum_{w \in C}\sum_{u \in Context(W) }logg(u) \\ =\sum_{w \in C}\sum_{u \in Context(W) }log\prod _{z \in \{u\} \bigcup NEG(u)}p(z|W) \\ =\sum_{w \in C}\sum_{u \in Context(W) } \{log[\sigma(v(W) ^T\Theta^u)]+\sum_{z \in NEG(u)}log[1-\sigma(v(W) ^T\Theta^u)]\}

可以看出来，这里需要对上下文中 Context(W) 的每一个词做一次负采样。实际上，作者在源码实现过程中并没有这么做，而是针对 w 进行了 |Context(W) | 次负采样，这样依赖，我们的目标函数变成

g(W) =\prod_{\tilde{w}\in Context(W) } \prod_{u \in {w}\bigcup NEG^{\tilde{w}}(W) }p(u|\tilde{w})

其中

p(u|\tilde{w})=\begin {cases} \sigma(v(W) ^T\Theta^u),&u=\tilde{w} \\ 1-\sigma(v(W) ^T\Theta^u),&u \neq \tilde{w}\end {cases}

这里 NEG^{\tilde{w}} (W) 表示处理词 \tilde{w} 时生成的负采样子集。

最终的目标函数变成

L =log\prod_{w \in C}g(W) =\sum_{w \in C}logg(W) \=\sum_{w \in C}log\{\prod_{\tilde{w}\in Context(W) } \prod_{u \in {w}\bigcup NEG^{\tilde{w}}(W) }p(u|\tilde{w})\} \\ =\sum_{w \in C}\sum_{\tilde{w}\in Context(W) }\{log\sigma(v(W) ^T\Theta^{\tilde{w}})+\sum_{u \in NEG^{\tilde{w}}(W) }\log[1-\sigma(v(W) ^T\Theta^u)]\}

考虑梯度更新，令

L(w,\tilde{w},u)=log\sigma(v(W) ^T\Theta^{\tilde{w}})+\sum_{u \in NEG^{\tilde{w}}(W) }\log[1-\sigma(v(W) ^T\Theta^u)]

所以

\frac{\partial L(w,\tilde{w},u)}{\partial \Theta^u}=\begin {cases}[1-\sigma(v(W) ^T\Theta^{\tilde{w}})]v(\tilde{w}), &u=\tilde {w} \-\sigma(v(W) ^T\Theta^{\tilde{w}})v(\tilde{w}),&u\neq \tilde{w} \end {cases}

\Theta^u:=\Theta^u+\eta \frac{\partial L(w,\tilde{w},u)}{\partial \Theta^u}

同理

\frac{\partial L(w,\tilde{w},u)}{\partial v(\tilde{w})}=\begin {cases}[1-\sigma(v(W) ^T\Theta^{\tilde{w}})]\Theta^{\tilde{w}}, &u=\tilde {w} \-\sigma(v(W) ^T\Theta^{\tilde{w}})\Theta^{\tilde{w}},&u\neq \tilde{w} \end {cases}

v(\tilde{w}):=v(\tilde{w})+\eta \sum_{u\in \{w\} \bigcup NEG^{\tilde{w}}(W) } \frac{\partial L(w,\tilde{w},u)}{\partial v(\tilde{w})}

3.2 Word2vec 不可忽视的问题

Word2vec 算法虽然在前些年取得了良好的效果，但是也有不足之处，其中最不可忽视的问题就是 一词多义 的问题。Word2vec 中最后对每一个词生成一个固定的向量表示，那么对于相同单词有多个含义时，就不能很好的解决。比如 bank，既有银行的意思，也有岸边的意思，当算法的结果只有一个固定向量对其进行表征时，必然导致这个词的表征不够准确。

既然存在问题，那就存在解决问题的方法，现在比较火的预训练相关的算法就解决了这个问题。具体咋�