贝壳找房基于内容热度的推荐
推荐系统本质上要拟合一个用户对内容满意度的函数[1],函数需要多个维度的特征包括:内容、用户等作为输入。个性化推荐建立在大量、有效的数据基础上。在建设初期,内容、用户的数据都还在积累,甚至对于数据的描述还是残缺不全[2]。在冷启动阶段,不妨把解决策略移到内容“热度”描述的算法上,使用"热度“算法对内容打分,由分数决定内容展示顺序。本文将从描述“热度”的视角介绍几种内容推荐策略,完成可解释性的推荐。
背景
眼动技术可以用于研究广告注意机制[3],其研究结果表明我们以特定的模式来浏览网页、手机屏幕[4],进而产生点击等进一步转化行为。其中的"F"模式常被人提及和关注,但在这种模式下如果某些关键内容刚好被用户跳过,则对于用户和内容提供者而言都是负向收益[5]。
 三个网页的用户眼动追踪热力图[4]> * 红-黄-蓝标记的区域,表示用户关注度依次降低;灰色则代表不会收到关注
三个网页的用户眼动追踪热力图[4]> * 红-黄-蓝标记的区域,表示用户关注度依次降低;灰色则代表不会收到关注
- 网页从左至右分别是:商业公司“about us”介绍页、购物网站详情页、搜索引擎结果页
在个性化推荐爆红之后,使用算法分发用户的“定制”内容来提高用户的点击行为已经成为信息平台等几乎所有软件的标配[1]。过度的推荐让用户停留在“信息茧房”[6]中,但我们还有另一个角度来实现推荐策略。即不考虑用户侧的隐私数据,按照对内容的评分无偏差的对用户进行展示,也就是本文即将描述的基于“热度”的可解释性推荐。
正文
正文部分将会展示一组描述内容“热度”的推荐策略,重点讨论用户反馈、时间衰减对热度分的影响,以上策略可应用在需要无差别曝光的内容推荐场景中。概括的讲,包含以下三个概念:
- 初始的热度分:内容入库时,利用对内容本身、内容的生产者的初步评估,可以得到内容初始的热度分。
- 热度变化:在内容曝光过程中,通过用户对内容的反馈产生正 or 负向的热度分。
- 热度时间衰减:为了体现时效性对内容曝光的影响还可以对热度分乘以一个随时间衰减的系数,或者直接加上某个随时间衰减的热度分。
1.使用用户正向投票
基于用户正向投票数:按照单位时间内用户对内容的正向投票绝对值,对内容进行降序排列。最直觉,也是最容易被理解的排名策略。
 旧版Delicious的“热门书签排行榜”[7]旧版 Delicious 的“热门书签排行榜”,就是按照单位时间内的用户正向投票数进行排名的,但是其策略是每间隔60分钟才进行一次排名操作。该策略优缺点都显而易见:* 优点:简单,每次更新排名迅速
旧版Delicious的“热门书签排行榜”[7]旧版 Delicious 的“热门书签排行榜”,就是按照单位时间内的用户正向投票数进行排名的,但是其策略是每间隔60分钟才进行一次排名操作。该策略优缺点都显而易见:* 优点:简单,每次更新排名迅速
- 缺点:统计周期内的热门内容持续“霸榜”,而在下一个周期里则可能一落千丈
2.引入连续时间衰减系数
Hacker News 是一个网络社区,可以张贴链接,或者讨论某个主题。其排名策略同时考虑用户正向投票数和时间因素[8]。
 Hacker News截图
Hacker News截图
Score = \frac{P-1}{(T+2)^G}
- P: 表示帖子得票数,P-1表示忽略发帖人的投票。
- T: 表示距离发帖的时间(单位为小时)。T+2可能是因为原始文章转贴至 Hacker News平均需要两个小时,所以+2还原最新帖子的实际发生时间。
- G: 表示“重力因子”(gravityth power,G > 1),即将帖子排名往下拉的力量。
得分公式可以看出:
- 帖子的票数 P-1 越多,内容的排名得分越高。可以在这一项上增加指数变为 {(P-1)}^\alpha ,增加( \alpha>1 )或减小( \alpha<0 )得票数对最终得分的影响。
- 随着发帖时间 T+2 的增长,内容的排名得分减小。而指数 G 用来调节发帖时间增长对排名得分的影响力度。通过调整G的大小,保证即使是热点新闻事件也会在设定的曝光时长后,平滑的退出排行榜首页。
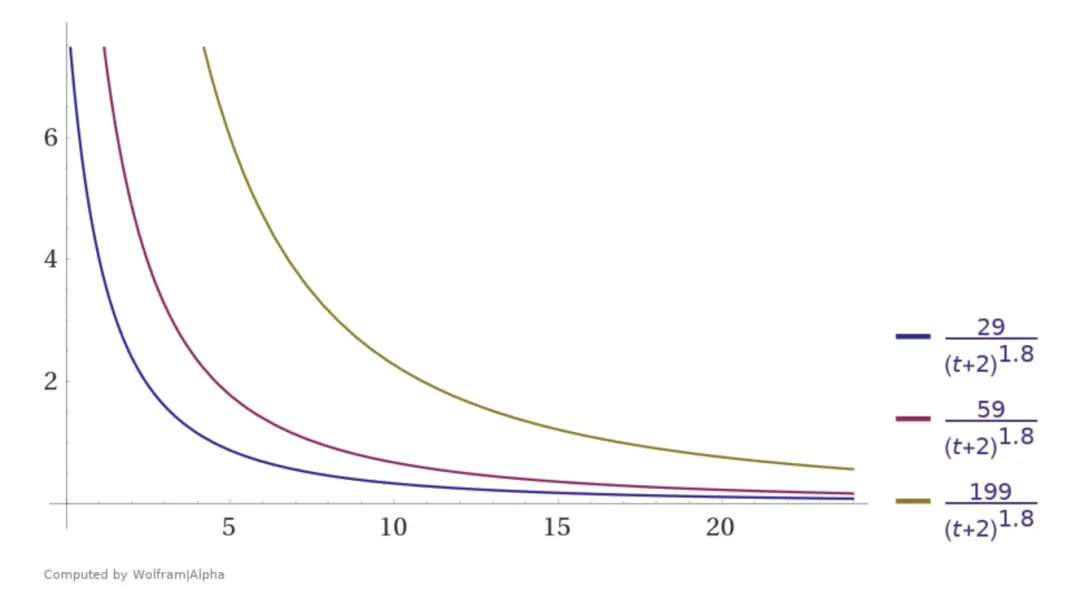
1.投票数对排名的影响:
plot(
(30 - 1) / (t + 2)^1.8,
(60 - 1) / (t + 2)^1.8,
(200 - 1) / (t + 2)^1.8
) where t=0..24
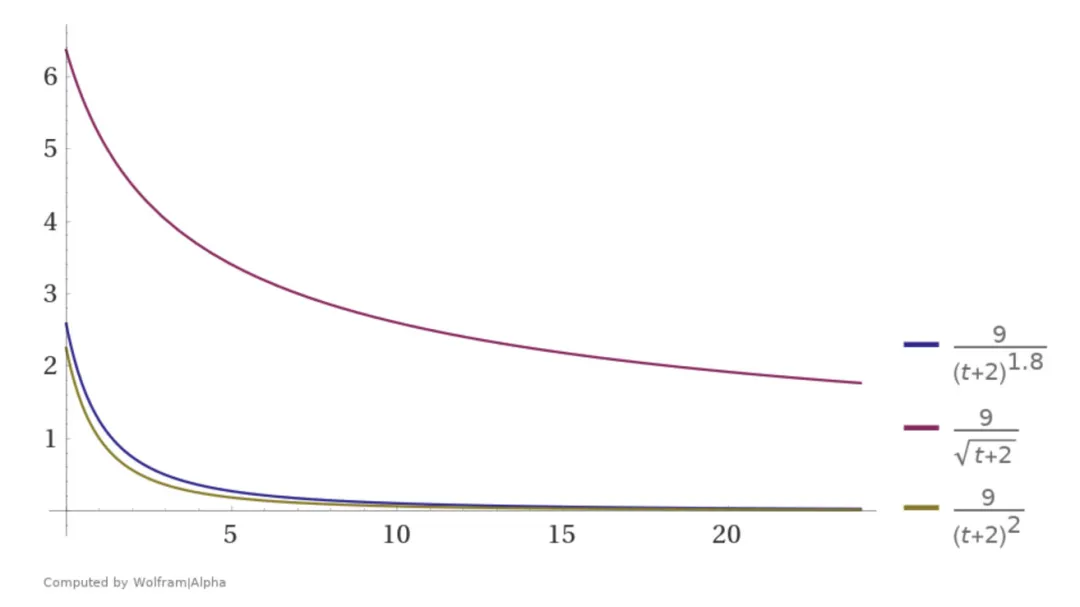
 2.重力因子G
2.重力因子G
plot(
(p - 1) / (t + 2)^1.8,
(p - 1) / (t + 2)^0.5,
(p - 1) / (t + 2)^2.0
) where t=0..24, p=10
3.引入反对票
Reddit[9]同时考虑赞同、和反对票,并且通过时间信息来加强这一点。
Score = log_{10} z + \frac{yt}{45000}
Cython代码[10]
cpdef double _hot(long ups, long downs, double date):
"""The hot formula. Should match the equivalent function in postgres."""
s = score(ups, downs) # 赞成票和反对票的差 x
order = log10(max(abs(s), 1)) # 受肯定、否定的程度 z
if s > 0: # 投票倾向sign, y
sign = 1
elif s < 0:
sign = -1
else:
sign = 0
seconds = date - 1134028003 # 文章新旧程度 t
return round(sign * order + seconds / 45000, 7) # 45000等于12.5小时
1.对数部分
- z表示,abs(赞成票-反对票)。z越大得分越高:即具有争议的主题,更加具有话题性,那么更容易带来重大影响,所以得分应该更高。
- 这里用的是以10为底的对数,z=10可以得到1分,z=100可以得到2分。这意味着前10分与和后来的90分(乃至紧接着的900分)会产生同样的权重。**“种子投票”会对得分产生重大影响力,越往后的投票贡献的力量越小**。这样可以保证即使是新产生的文章也可以迅速获得分数、得到曝光;但同时不会产生某个文章突然爆红的现象。
2.分数部分
- t越大,得分越高: 新文章得分会高于老文章。
- 分母 45000 秒,等于 12.5 个小时。即新帖比25小时前的文章自动高 2 分。结合对数部分,如果旧文章想在25小时继续保持原先的得分,在25小时内它的 z 值必须增加 100 倍。
- y 的作用是决定加分或减分。 天然的让得到大量净赞成票的文章排名靠前,赞成票与反对票接近或相等的文章其次,得到净反对票的文章会排在最后。
4.更加泛化的牛顿冷却定律
这是一个更一般的数学模型。我们可以把"热文排名"想象成一个"自然冷却"的过程[11]:
-
任一时刻,网站中所有的文章,都有一个“当前温度”,温度最高的文章就排在第一位。
-
如果一个用户对某篇文章投了赞成票(或评论 等其他操作),该文章的温度就上升一度。
-
随着时间流逝,所有文章的温度都逐渐“冷却”,而且冷却的速度和当前温度-初始温度的差值成正比。
T^‘(t)=-\alpha(T(t)-H)
这样假设的意义在于,我们可以照搬物理学的冷却定律,使用现成的公式,建立“温度”与“时间”之间的函数关系,构建一个“指数式衰减(Exponential decay)”过程。
求解微分方程后,得到:
T = T_0 e^{-\alpha(t-t_0)}
将这个公式用在"排名算法",就相当于(假定本期没有增加净赞成票)时:**本期得分 = 上一期得分 x exp(-(冷却系数) x 间隔的小时数)。**而如果假定一篇新文章的初始分数是100分,24小时之后"冷却"为1分,那么可以计算得到"冷却系数"约等于0.192。
简单来说,如果选择牛顿冷却,需要以下几步:
1. 设定新文章的初始温度
2. 设定冷却速度
3. 设定温度增加的方式
4. 当某项有赞成票时,触发并重新计算当前温度,并记录当前时间
5. 使用以上公式根据当前温度对项目进行排序
5.引入文章评论、浏览对文章排名的影响
Stack Overflow 引入了问题评论对问题热度排名的影响[12]。一旦有人回答了某个问题,其他人可以对这个回答投票(赞成 or 反对),以表明对这个回答的态度。通过评论也可以找出某段时间内的热点问题:即哪些问题最被关注、得到了最多的讨论。
 StackOverflow网站
StackOverflow网站
\frac{(log_{10} Qviews)*4 + \frac{Qanswers*Qscore}{5} + sum(Ascores)} {((Qage+1) - \frac{Qage-Qupdated}{2})^{1.5}}
- 问题的浏览次数Qviews:以10为底的对数;10得一分、100得两分,即后来者影响力变小
- Qscore = 赞成票-反对票。如果某个问题越受到好评,排名自然应该越靠前;
- Qanswers 表示回答的数量,代表有多少人参与这个问题。这个值越大,得分将成倍放大。Qanswers 就等于0,这时Qscore 再高也没用,意味着再好的问题,也必须有人回答,否则进不了热点问题排行榜。
- 回答得分 Ascores:“回答”比“问题”更有意义。得分越高,代表回答的质量越高。
- 距离问题发表的时间Qage和距离最后一个回答的时间 Qupdated,单位是秒。随着时间流逝,这两个值都会越变越大,导致分母增大,因此总得分会越来越小。
Stack Overflow 热点问题的排名,与参与度(Qviews 和 Qanswers)和质量(Qscore 和 Ascores)成正比,与时间(Qage 和 Qupdated)成反比。
6.引入置信度
Reddit评论排名算法工作原理[9]:
- ‘热门‘排名算法对评论进行排名不是很有效,它会显得对早期的评论过于偏爱。
- 在一个评论系统中,我们的目的是找出最佳评论,不论它是什么时间提交的。
- 1927年Edwin B. Wilson找到了一种很好的算法,被叫做”Wilson score interval”,它可以被用于“信任排序(the confidence sort)”[13]。信任排序把文章的获得的票数当作全体读者的一个抽样统计——就像一次民意测验。
我们一点点分析,最后再到最后的Wilson score interval算法。
常见带有偏置的策略:
- 得分 = 赞成票 - 反对票
假定有两个项目,项目A是60张赞成票,40张反对票,项目B是550张赞成票,450张反对票。请问,谁应该排在前面?按照上面的公式,B会排在前面,因为它的得分(550 - 450 = 100)高于A(60 - 40 = 20)。但是实际上,B的好评率只有55%(550 / 1000),而A为60%(60 / 100),所以正确的结果应该是A排在前面
- 得分 = 赞成票 / 总票数
如果"总票数"很大,这种算法其实是对的。问题出在如果"总票数"很少,这时就会出错。假定A有2张赞成票、0张反对票,B有100张赞成票、1张反对票。这种算法会使得A排在B前面。这显然错误。
这个问题可以换另一个角度看待,使用二项分布:
- 每个用户的投票都是独立事件。
- 用户只有两个选择,要么投赞成票,要么投反对票。
- 如果投票总人数为n,其中赞成票为k,那么赞成票的比例p就等于k/n。
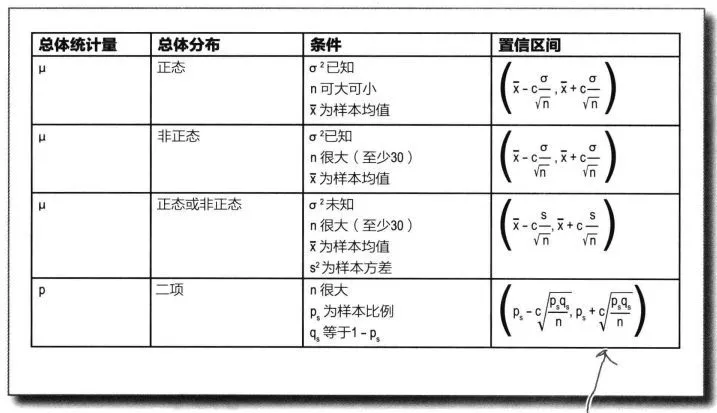
思路是,p越大,就代表这个项目的好评比例越高,越应该排在前面。但p的可信性,取决于有多少人投票,如果样本太小,p就不可信。好在我们已经知道,p是二项分布中某个事件的发生概率,因此我们可以计算出p的置信区间。所谓“置信区间”,就是说,以某个概率而言,p会落在的那个区间。比如,某个产品的好评率是 80%,但是这个值不一定可信。根据统计学,我们只能说,有95%的把握可以断定,好评率在 75%~85%之间,即置信区间是 [75%, 85%]。
对于置信区间的计算?
- 做正太近似[14]
如果n足够大,那么分布的偏度就比较小。在这种情况下,如果使用适当的连续性校正,那么B(n,p)的一个很好的近似是正态分布:N(np,np(1-p))。常用的 规则是要求np和n(1 −p)都必须大于 5。
由于选取样本不同,表达的是一个误差范围,是对总体统计量给出一个区间估计。置信水平,即为观测值处于置信区间中的概率估计[18]。
 1. Wilson score interval算法
1. Wilson score interval算法
1927年,美国数学家 Edwin Bidwell Wilson提出了一个修正公式,被称为“威尔逊区间”,很好地解决了小样本的准确性问题[15]。它的数学表达式是这样的:
\frac{\widehat{p}+\frac{1}{2n}z^2_{1-\frac{\alpha}{2}}\pm z_{1-\frac{\alpha}{2}}\sqrt{ \frac{\widehat{p} (1 - \widehat{p} )}{n} + \frac{z^2_{1-\frac{\alpha}{2}}} {4n^2}}}{{1+\frac{1}{n}z^2_{1-\frac{\alpha}{2}}} }
在上面的公式中,\widehat{p}表示样本的”赞成票比例”,n表示样本的大小,z表示对应某个置信水平的z统计量,这是一个常数,可以通过查前文表得到。一般情况下,在95%的置信水平下,z统计量的值为1.96。
威尔逊置信区间的均值为:
\frac{\widehat{p}+\frac{1}{2n}z^2_{1-\frac{\alpha}{2}}}{{1+\frac{1}{n}z^2_{1-\frac{\alpha}{2}}} }
下限为:
\frac{\widehat{p}+\frac{1}{2n}z^2_{1-\frac{\alpha}{2}} - z_{1-\frac{\alpha}{2}}\sqrt{ \frac{\widehat{p} (1 - \widehat{p} )}{n} + \frac{z^2_{1-\frac{\alpha}{2}}} {4n^2}}}{{1+\frac{1}{n}z^2_{1-\frac{\alpha}{2}}} }
可以看到: 当的值足够大时,这个下限值会趋向。如果非常小(投票人很少),这个下限值会大大小于,实际上,起到了降低”赞成票比例”的作用,使得该项目的得分变小、排名下降。
7.贝叶斯平均
“威尔逊区间”解决了投票人数过少、导致结果不可信的问题。如果只有 2 个人投票,“威尔逊区间”的下限值会将赞成票的比例大幅拉低。这样做固然保证了排名的可信性,但也带来了另一个问题:排行榜前列总是那些票数最多的项目,新项目或者冷门的项目,很难有出头机会,排名可能会长期靠后[16]。
热门电影与冷门电影的平均得分,是否真的可比?举例来说,一部好莱坞大片有 10000 个观众投票,一部小成本的文艺片只有 100 个观众投票。这两者的投票结果,怎么比较?如果使用“威尔逊区间”,后者的得分将被大幅拉低,这样处理是否公平,能不能反映它们真正的质量?
设法为低投票结果,设法为它增加一些投票: 既然不知道投票结果,那就先估计一个值,然后不断用新的信息修正,使得它越来越接近正确的值。
WR=\frac{v}{v+m}R + \frac{m}{v+m}C
- WR,加权得分(weighted rating)。
- R,该电影的用户投票的平均得分(Rating)。
- v,该电影的投票人数(votes)。
- m,排名前250名的电影的最低投票数(设为3000)。
- C, 所有电影的平均得分(设为6.9)。
仔细研究这个公式,你会发现,IMDB [17] [18]为每部电影增加了 3000 张选票,并且这些选票的评分都为 6.9。这样做的原因是,假设所有电影都至少有 3000 张选票,那么就都具备了进入前250名的评选条件;然后假设这 3000 张选票的评分是所有电影的平均得分(即假设这部电影具有平均水准);最后,用现有的观众投票进行修正,长期来看,v/(v+m)这部分的权重将越来越大,得分将慢慢接近真实情况。
这样做拉近了不同电影之间投票人数的差异,使得投票人数较少的电影也有可能排名前列。在这个公式中,m(总体平均分)是"先验概率",每一次新的投票都是一个调整因子,使总体平均分不断向该项目的真实投票结果靠近。投票人数越多,该项目的"贝叶斯平均"就越接近算术平均,对排名的影响就越小。
总结
热度排名由3个方面影响:
- 初始状态热度(文章来源、类别、作者的信息等)
- 热度如何上升(点赞、收藏、关注、评论等)
- 热度如何下降(反对、低评分、时间增长等)
但对于不同类型的网站,内容的热度排名显然有不同的侧重点。对于工具性的网站,如StackOverflow,他的热度计算方法会让有价值内容的排名随着时间推移慢慢上升;而新闻类关注时效性的网站,则需要让热点内容排名的在有效时间后快速下降。
总之,选择什么样的热度排名计算方式取决于产品的定位,没有最好只有最合适。对于可解释性较强的热度排名也可以根据产品要求不断调整,适应用户口味和产品定位。
参考
2.产品经理需要了解的算法——热度算法和个性化推荐( http://www.woshipm.com/pmd/723735.html)
3.周象贤;金志成. 国外对平面广告受众注意心理的眼动研究[J]. 心理科学进展, 2006, 14(02): 287-.
4.F-Shaped Pattern For Reading Web Content (original study)( https://www.nngroup.com/articles/f-shaped-pattern-reading-web-content-discovered/)
5.F-Shaped Pattern of Reading on the Web: Misunderstood, But Still Relevant (Even on Mobile)( https://www.nngroup.com/articles/f-shaped-pattern-reading-web-content/)
6.人民网二评算法推荐:别被算法困在“信息茧房”( http://opinion.people.com.cn/n1/2017/0919/c1003-29544724.html)
7.基于用户投票的排名算法(一):Delicious和Hacker News( http://www.ruanyifeng.com/blog/2012/02/ranking_algorithm_hacker_news.html)
8.Hacker News 排名算法工作原理( https://www.aqee.net/post/how-hacker-news-ranking-algorithm-works.html)
9.Reddit排名算法工作原理( https://www.aqee.net/post/how-reddit-ranking-algorithms-work.html)
11.Rank Hotness With Newton’s Law of Cooling( https://www.evanmiller.org/rank-hotness-with-newtons-law-of-cooling.html)
12.What formula should be used to determine “hot” questions?( https://meta.stackexchange.com/questions/11602/what-formula-should-be-used-to-determine-hot-questions)
13.《How Not To Sort By Average Rating》( [http://www.evanmiller.org/how-not-to-sort-by-average-rating.html](https://zshipu.com/t?url=http%3A%2F%2Fwww.evanmiller.org%2Fh
- 原文作者:知识铺
- 原文链接:https://index.zshipu.com/geek/post/%E4%BA%92%E8%81%94%E7%BD%91/%E8%B4%9D%E5%A3%B3%E6%89%BE%E6%88%BF%E5%9F%BA%E4%BA%8E%E5%86%85%E5%AE%B9%E7%83%AD%E5%BA%A6%E7%9A%84%E6%8E%A8%E8%8D%90/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


