算法详解原理推导及应用
本文转载自SigAI 公众号
与随机森林一样,Boosting算法也是一种集成学习算法,随机森林和集成学习在SIGAI之前的公众号文章“随机森林概述”中已经介绍。Boosting的分类器由多个弱分类器组成,预测时用每个弱分类器分别进行预测,然后投票得到结果;训练时依次训练每个弱分类器,每个弱分类器重点关注被前面的弱分类器错分的样本。弱分类器是很简单的分类器,它计算量小且精度不用太高。
AdaBoost算法由Freund等人于1995年提出,是Boosting算法的一种实现,与SVM一样,在其发明后的10多年里,得到了成功的应用。在今天的文章中,我们将和大家一起回顾这一种当年在历史上有过辉煌成就的经典算法。
在基本的AdaBoost算法中,每个弱分类器都有权重,弱分类器预测结果的加权和形成了最终的预测结果。训练时,训练样本也有权重,在训练过程中动态调整,被前面的弱分类器错分的样本会加大权重,因此算法会关注难分的样本。2001年,级联的AdaBoost分类器被成功用于人脸检测问题,此后它在很多模式识别问题上得到了成功的应用。
AdaBoost算法简介
AdaBoost算法的全称是自适应Boosting(Adaptive Boosting),是一种二分类器,它用弱分类器的线性组合构造强分类器。弱分类器的性能不用太好,只需要比随机猜测强,依靠它们可以构造出一个非常准确的强分类器。强分类器的计算公式为:
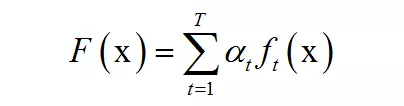
其中x是输入向量,F(x)是强分类器,ft(x)是弱分类器,αt是弱分类器的权重值,是一个正数,T为弱分类器的数量。弱分类器的输出值为+1或-1,分别对应于正样本和负样本。分类时的判定规则为:
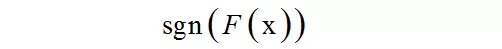
其中sgn是符号函数。强分类器的输出值也为+1或-1,同样对应于正样本和负样本。弱分类器和它们的权重值通过训练算法得到。之所以叫弱分类器是因为它们的精度不用太高。
训练算法
训练时,依次训练每一个弱分类器,并得到它们的权重值。训练样本同样带有权重,初始时所有样本的权重相等,被前面的弱分类器错分的样本会加大权重,反之会减小权重,因此接下来的弱分类器会更加关注这些难分的样本。弱分类器的权重值根据它的准确率构造,精度越高的弱分类器权重越大。给定l个训练样本(xi,yi),其中xi是特征向量,yi为类别标签,其值为+1或-1。训练算法的流程如下:
初始化样本权重值,所有样本的初始权重相等:
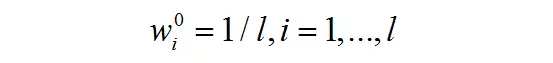
循环,对t=1,…,T依次训练每个弱分类器:
训练一个弱分类器ft(x),并计算它对训练样本集的错误率et
计算弱分类器的权重:
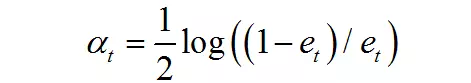
更新所有样本的权重:
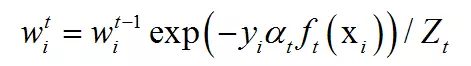
其中Zt为归一化因子,它是所有样本的权重之和:
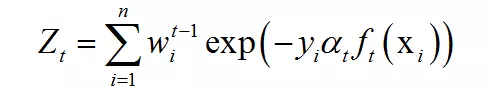
结束循环
最后得到强分类器:
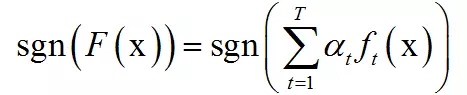
根据弱分类器权重的计算公式,错误率低的弱分类器权重大,它是准确率的增函数。在SIGAI之前的公众号文章“大话AdaBoost算法”中,我们给出了一个形象的例子。每个弱分类器类似于一个水平不太高的医生,如果在之前的考核中一个医生的技术更好,对病人情况的判断更准确,那么可以加大他在会诊时说话的分量即权重。而强分类器就是这些医生的结合。
给训练样本加权重是有必要的,如果样本没有权重,每个弱分类器的训练样本是相同的,训练出来的弱分类器也是一样的,这样训练多个弱分类器没有意义。AdaBoost算法的原则是:
关注之前被错分的样本,准确率高的弱分类器有更大的权重。
上面的算法中并没有说明弱分类器是什么样的,具体实现时我们应该选择什么样的分类器作为弱分类器?一般用深度很小的决策树。强分类器是弱分类器的线性组合,如果弱分类器是线性函数,无论怎样组合,强分类器都是线性的,因此应该选择非线性的分类器做弱分类器。
训练算法的推导
AdaBoost看上去是一个脑洞大开想出来的算法,你可能会问:为什么弱分类器的权重计算公式是这样的?为什么样本权重的更新公式是这样的?事实上,它们是有来历的。我们可以用广义加法模型+指数损失函数来推导出AdaBoost的训练算法。
广义加法模型拟合的目标函数是多个基函数的线性组合:
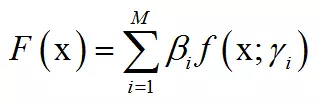
其中
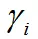 为基函数的参数,
为基函数的参数,
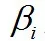 为基函数的权重系数。训练时这个模型要确定的是基函数的参数和权重值。训练的目标是最小化对所有样本的损失函数:
为基函数的权重系数。训练时这个模型要确定的是基函数的参数和权重值。训练的目标是最小化对所有样本的损失函数:
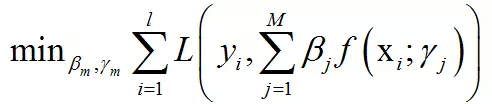
训练算法依次确定每个基函数的参数和它们的权重。接下来将从广义加法模型推导出AdaBoost的训练算法。首先定义强分类器对单个训练样本的损失函数:
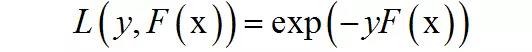
这是指数损失函数。如果标签值与强分类器的预测值越接近,损失函数的值越小,反之越大。使用指数损失函数而不用均方误差损失函数的原因是均方误差损失函数对分类问题的效果不好。将广义加法模型的拟合函数代入指数损失函数中,得到算法训练弱分类器时要优化的目标函数为:
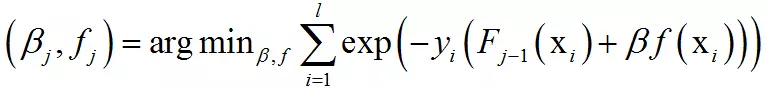
这里将指数函数拆成了两部分,已有的强分类器,以及当前弱分类器对训练样本的损失函数,前者在之前的迭代中已经求出,可以看成常数。目标函数可以简化为:
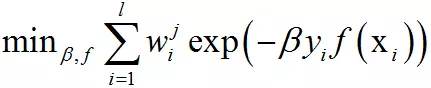
其中:
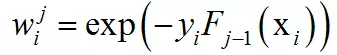
它只和前面的迭代得到的强分类器有关,与当前的弱分类器、弱分类器权重无关,这就是样本权重。这个最优化问题可以分两步求解,首先将
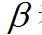 看成常数,由于yi和f(xi)的取值只能为+1或-1,要让上面的目标函数最小化,必须让二者相等。因此损失函数对f(x)的最优解为:
看成常数,由于yi和f(xi)的取值只能为+1或-1,要让上面的目标函数最小化,必须让二者相等。因此损失函数对f(x)的最优解为:
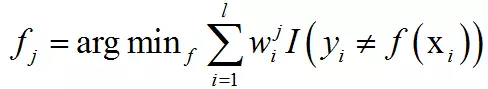
其中I是指标函数,根据括号里的条件是否成立其取值为0或1。上式的最优解是使得对样本的加权误差率最小的分类器。得到弱分类器之后,优化目标可以表示成
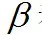 的函数:
的函数:
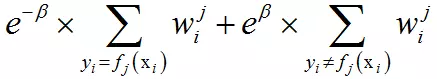
上式前半部分是被正确分类的样本,后半部分是被错误分类的样本。这可以写成:
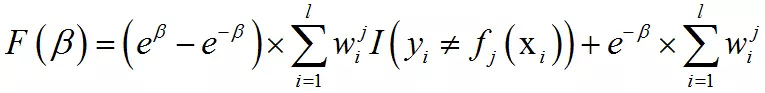
具体推导过程为:
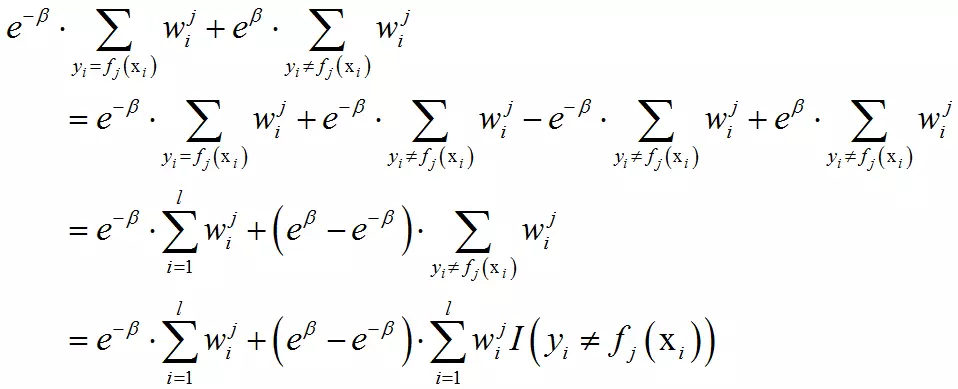
函数在极值点的导数为0,即:
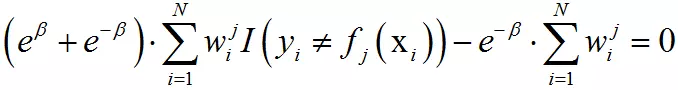
由此得到关于
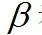 的方程:
的方程:
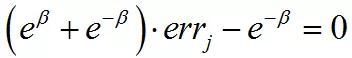
最优解为:
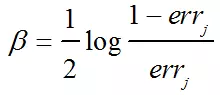
其中errj为弱分类器对训练样本集的加权错误率:
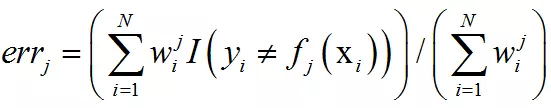
对逼近函数做如下更新:
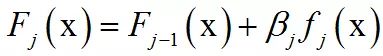
导致下次迭代时样本的权重为:
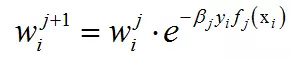
这就是样本权重的更新公式。AdaBoost训练算法就是求解上述最优化问题的过程。
实际应用
AdaBoost算法最成功的应用之一是机器视觉里的目标检测问题,如人脸检测和行人检测。车辆检测。在深度卷积神经网络用于此问题之前,AdaBoost算法在视觉目标检测领域的实际应用上一直处于主导地位。
在2001年Viola和Jones设计了一种人脸检测算法。它使用简单的Haar特征和级联AdaBoost分类器构造检测器,检测速度较之前的方法有2个数量级的提高,并且有很高的精度,我们称这种方法为VJ框架。VJ框架是人脸检测历史上有里程碑意义的一个成果,奠定了AdaBoost目标检测框架的基础。
用级联AdaBoost分类器进行目标检测的思想是:用多个AdaBoost分类器合作完成对候选框的分类,这些分类器组成一个流水线,对滑动窗口中的候选框图像进行判定,确定它是人脸还是非人脸。在这些AdaBoost分类器中,前面的分类器很简单,包含的弱分类器很少,可以快速排除掉大量非人脸窗口,但也可能会把一些不是人脸的图像判定为人脸。如果一个候选框通过了第一级分类器的筛选即被它判定为人脸,则送入下一级分类器中进行判定,否则丢弃掉,以此类推。如果一个检测窗口通过了所有的分类器,则认为是人脸,否则是非人脸。
这种思想的精髓在于用简单的强分类器先排除掉大量的非人脸窗口,使得最终能通过所有级强分类器的样本数很少。这样做的依据是在待检测图像中,绝大部分都不是人脸而是背景,即人脸是一个稀疏事件,如果能快速的把非人脸样本排除掉,则能大大提高目标检测的效率。
出于性能的考虑,弱分类器使用了简单的Haar特征。这种特征源自于小波分析中的Haar小波变换,Haar小波是最简单的小波函数,用于对信号进行均值、细节分解。这里的Haar特征定义为图像中相邻矩形区域像素之和的差值。下图是基本Haar特征的示意图:
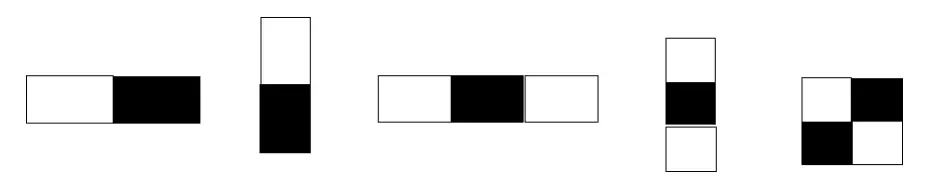
Haar特征是白色矩形框内的像素值之和,减去黑色区域内的像素值之和。以图像中第一个特征为例,它的计算方法如下:首先计算左边白色矩形区域里所有像素值的和,接下来计算右边黑色矩形区域内所有像素的和,最后得到的Haar特征值为左边的和减右边的和。
这种特征捕捉图像的边缘、变化信息,各种特征描述在各个方向上的图像变化信息。人脸的五官等区域有各自的亮度信息,很符合Haar特征的特点。
为了实现快速计算,使用了一种称为积分图的机制。通过它可以快速计算出图像中任何一个矩形区域的像素之和,从而计算出各种类型的Haar特征。假设有一张图像,其第i行第j列处的像素值为xij,积分图定义为:
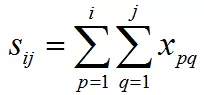
即图像在任何一点处的左上方元素之和。在构造出积分图之后,借助于它可以快速计算出任何一个矩形区域内的像素之和。以下图中的黑色矩形框为例:
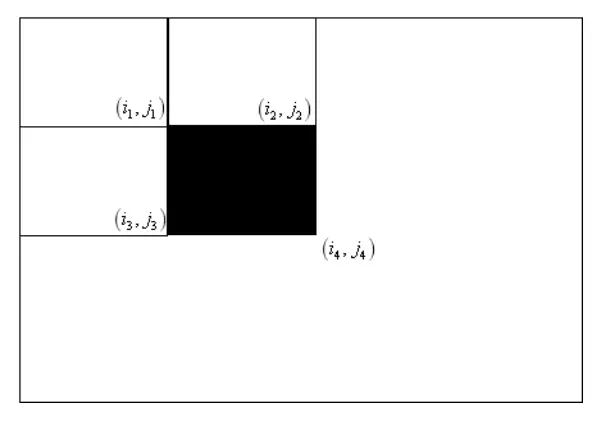
在上图中,要计算黑色矩形框内的像素值之和,计算公式为:
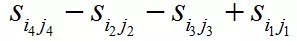
所以这样,是因为黑色区域内的像素值之和等于这4个矩形框内的像素值之和,减去上面两个矩形框的像素值之和,再减去左边两个矩形框的像素值之和,这样做的话,左上角的矩形
- 原文作者:知识铺
- 原文链接:https://index.zshipu.com/geek/post/%E4%BA%92%E8%81%94%E7%BD%91/%E7%AE%97%E6%B3%95%E8%AF%A6%E8%A7%A3%E5%8E%9F%E7%90%86%E6%8E%A8%E5%AF%BC%E5%8F%8A%E5%BA%94%E7%94%A8/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


