本次课程的主题包括：

  1. Web structure
  2. Pagerank 推导和计算方式
  3. 应用：Graph Search（个人认为反而是重要的部分）

1. Web Structure

1.1 定义：有向图

: 所有能够到达 v 的节点集合

：所有 v 能够到达的节点集合

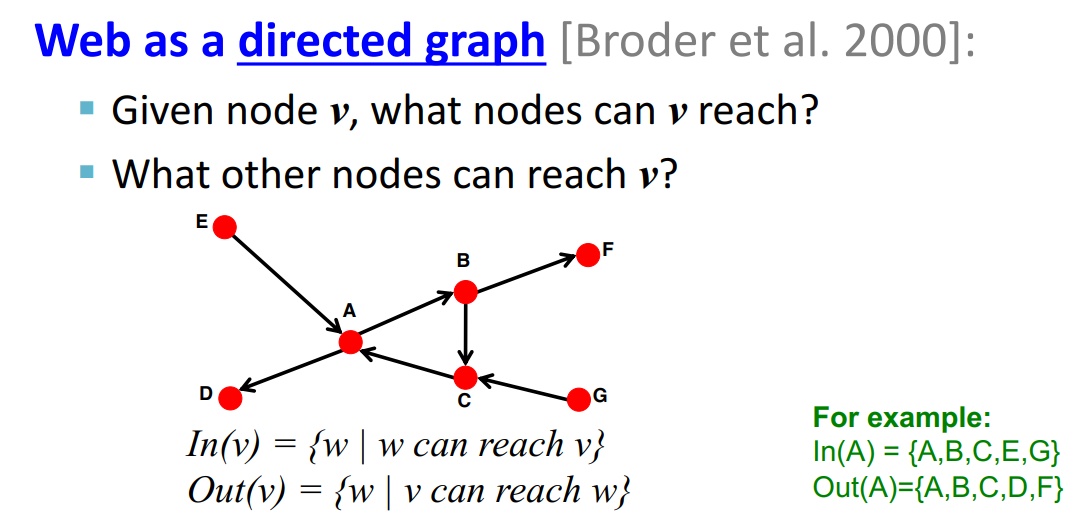
有向图的两种类别：

strongly connected：节点间是互通的，能够通过有向路径实现互达

（ ）

directed acyclic graph：有向无环图，u 可以达到 v，但 v 不能到达 u

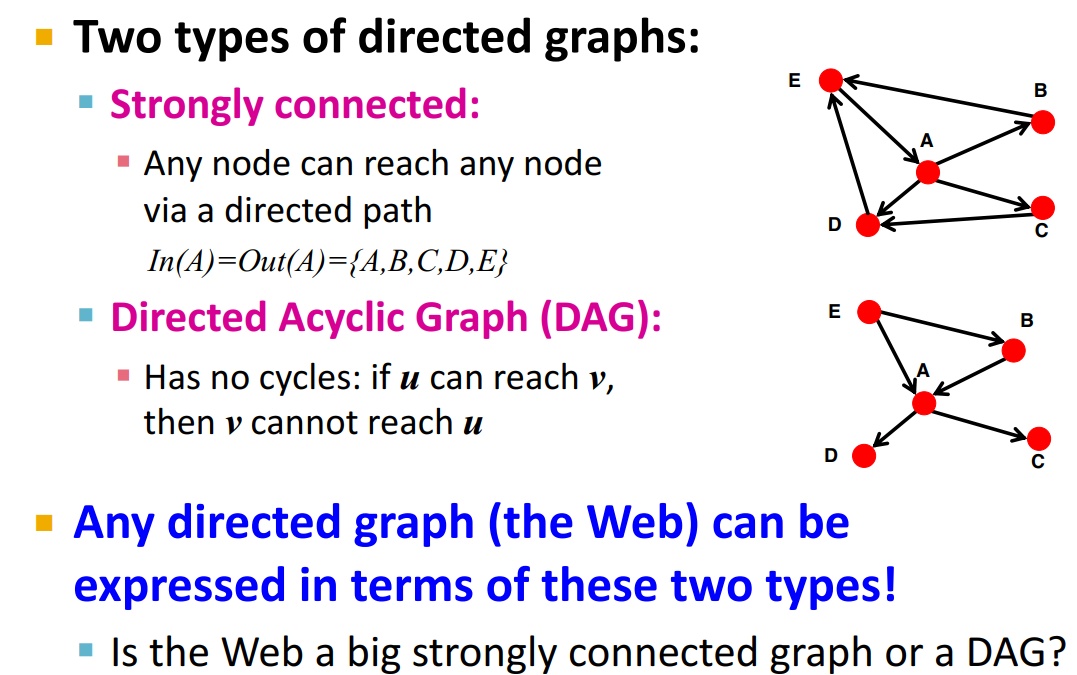
Strongly connected component

  1. 这个集合内节点可以互达
  2. 这已经是最大的满足这种要求的集合，不能更大了

每一个有向图都是在 SCC 上构成的 DAG

意思是说，如果把有向图中能够互达的节点集合揉成一个新结点，那么就是一个 DAG 了

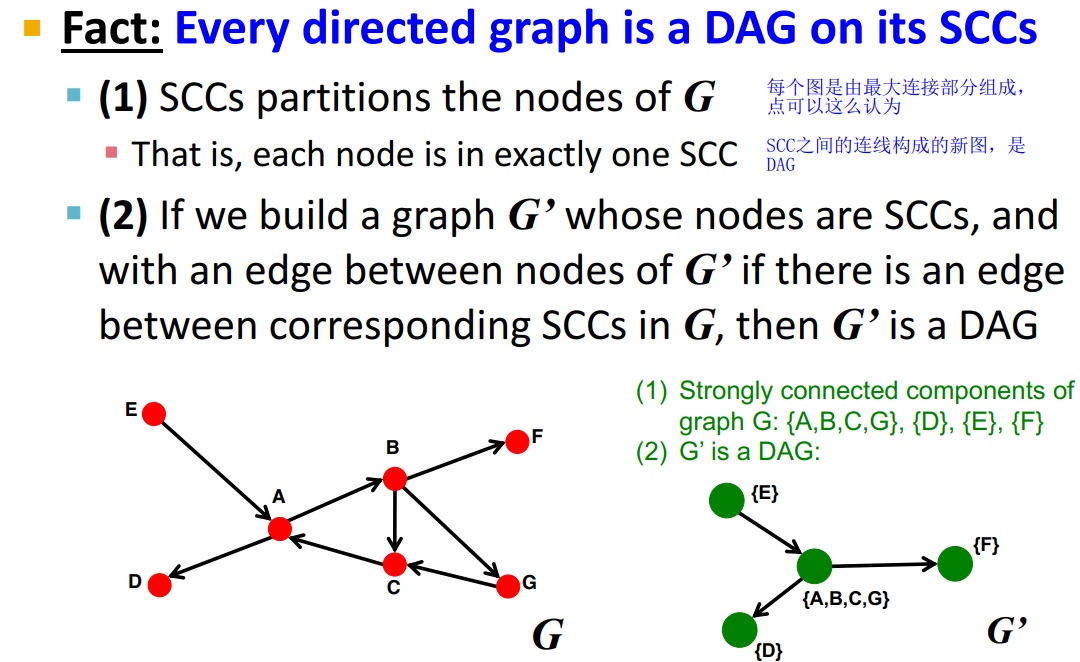
问题来了：想看看真是 Web 网络，是如何在其 SCC 上构成整个 DAG 图的？

  1. 首先，对于一个节点 v，如何找到包含这个 v 的 SCC？

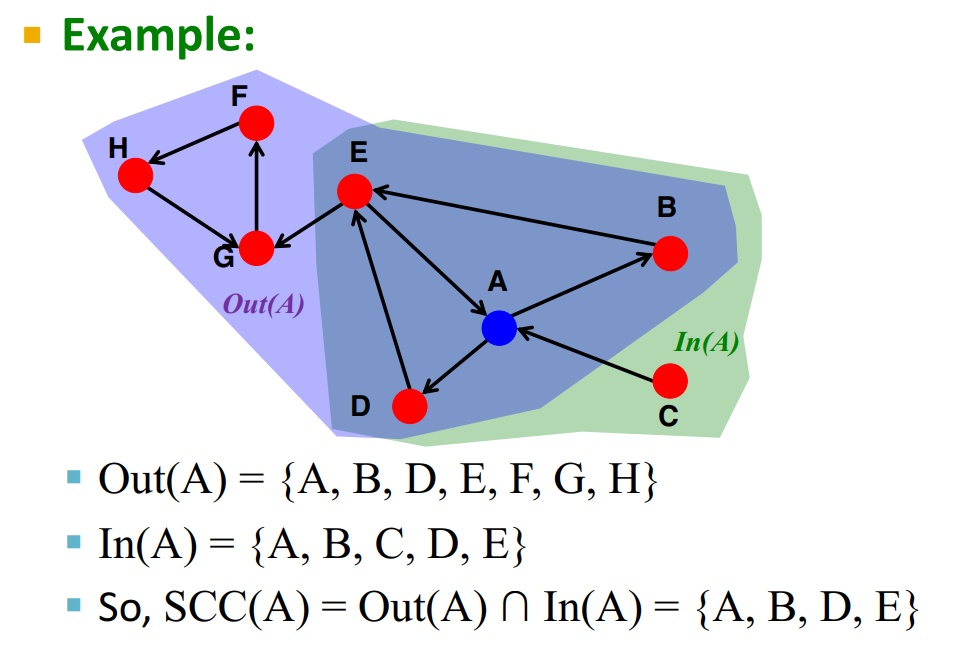
定义：

是 G 的反向图

2. 实验结果

  • 数据来源：爬取的网络结构，2.03 亿 urls，15 亿 links
  • 方法：任意节点 v，使用 BFS 策略（宽度优先）计算 In(v)和 Out(v)
  • 观察结果：BFS 策略要么访问极少的节点，要么可以访问居多的节点

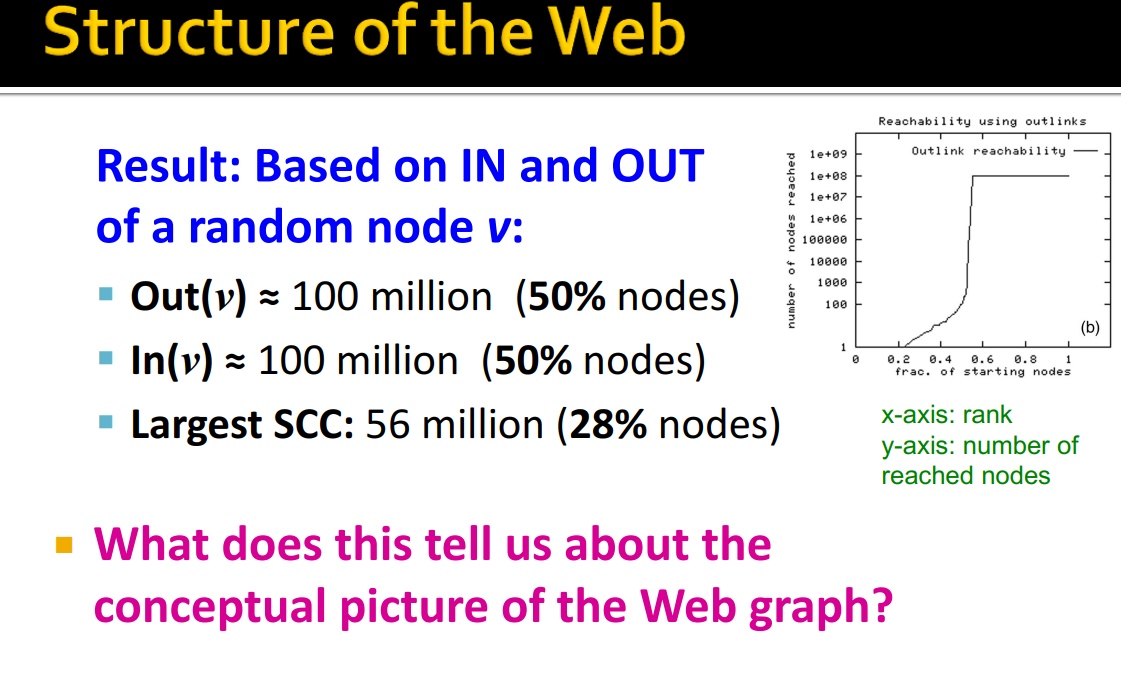
说明，网络结构是一个领带形式的玩意。

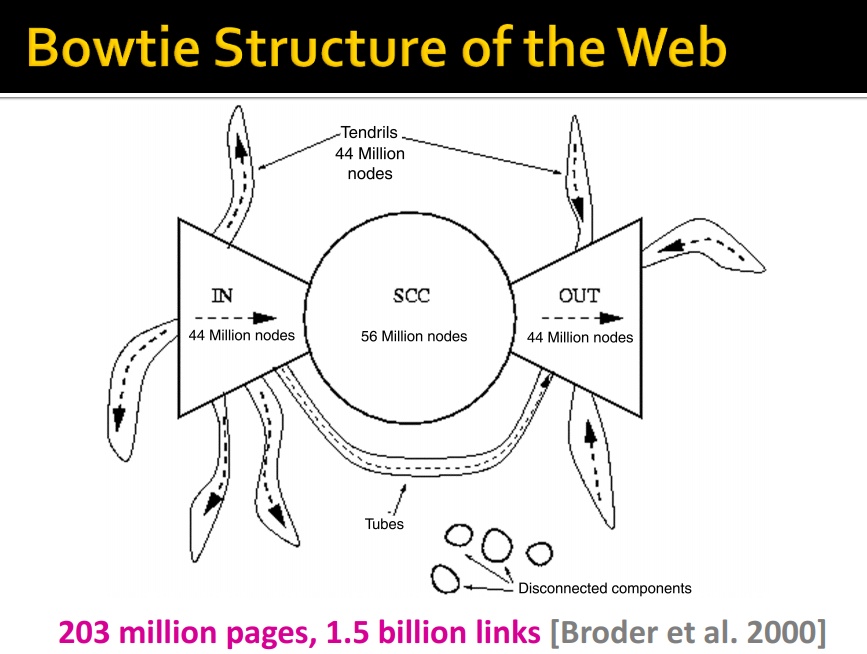
2. Ranking nodes on the graph

Intuition：网络中不同节点的重要度肯定是不同的，stanford vs 野鸡大学

所以，我们要排序！

rank the pages using the Web graph link structure

Link Analysis Algorithms

  • pagerank
  • personalized pagerank
  • random walk with restarts

PageRank

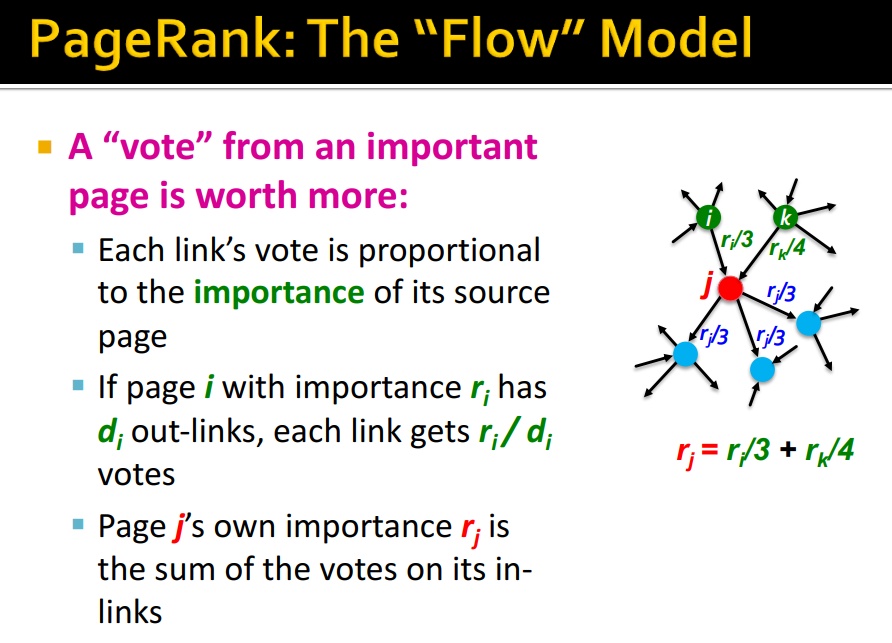
Idea：将 link 视为 votes，链接越多越重要

还有一个问题，所有链接都一样吗？

那肯定不行啊，杀人游戏中，警长还有两票的投票权呢

从重要节点投出的票会更加重要！

那怎么分配链接上的权重呢？ 平均

  • 对于 page with importance ,有 个外向连接（出度），那每个链接得到的投票权为：
  • 对于节点 ，其重要度就是所有指向它的投票权之和：

用矩阵定义这种形式，引入 邻接矩阵 M

如果 ， 的出度为 ，那么

M 的列和为 1，表示所有从 j 出去的投票权

rank vector r：每个节点的重要度

矩阵形式：

接下来的论述是，设想是一个 surfer 在这样的 Web 上一直随机游走，最后停留在各个页面上的概率

这样论述的目的在于得到一个概率形式：

那么 就是最后的稳态概率，对应意义说各个节点重要度也会收敛起来

这可以有两个解释：

1、马尔可夫过程的收敛

其实给定矩阵 ，计算 的过程就是一个重复的过程，

相当于是一个马尔可夫链最后的收敛状态

2、特征值分解

对比一下，其实就是特征值为 1 的特征向量！

工业上如何求得 r 呢？——Power Iteration Method

迭代过程很简单：三步

  • 初始化：
  • 迭代：
  • 终止条件：

L1 范数约束

示例：

写到这里，不得不思考几个问题：

  • 这个计算模式，它最后收敛吗？
  • 如果能够收敛，是否收敛到我们想要的值？
  • 结果合理吗？

Pagerank 有两个小问题需要解决

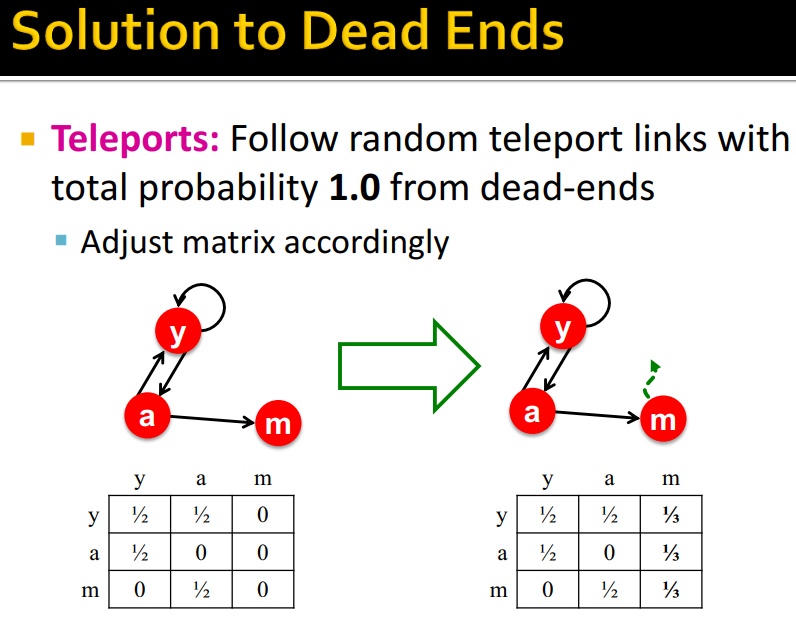
1、dead ends：有些网页不能往外链接了，也就是断头路

如图，所有重要度都变成 0

解决方式：以概率 1.0 转移到其他节点

需要调整邻接矩阵

2、spider trap：陷入局部循环了，一直在一个圈里打转，导致 importance 计算不正常

如图，a 重要度变成 0，b 成了 1

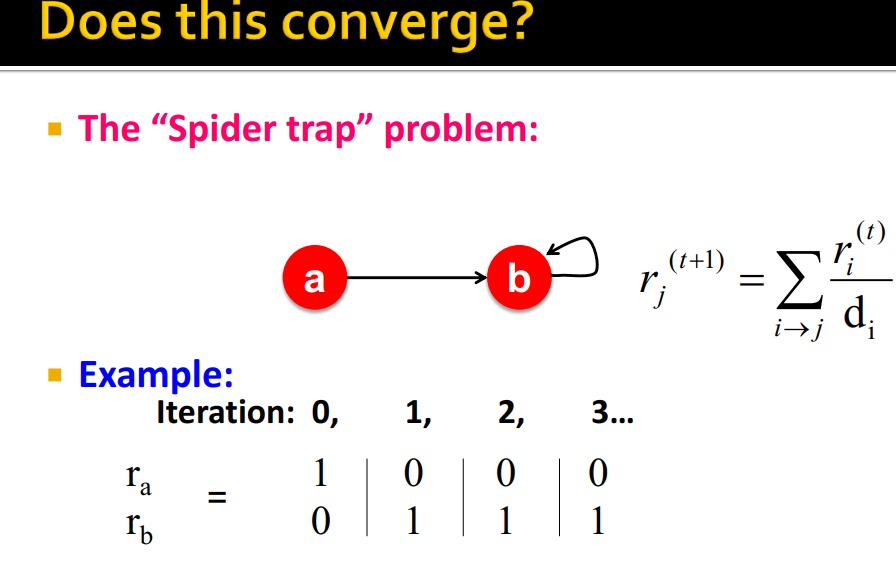
解决方式：跳出这种问题

  • 概率 的可能继续随机走
  • 概率 的可能跳转到其他随机页面

值在 0.8-0.9 之间

如何，在经历几步后，能够瞬移出 spider trap

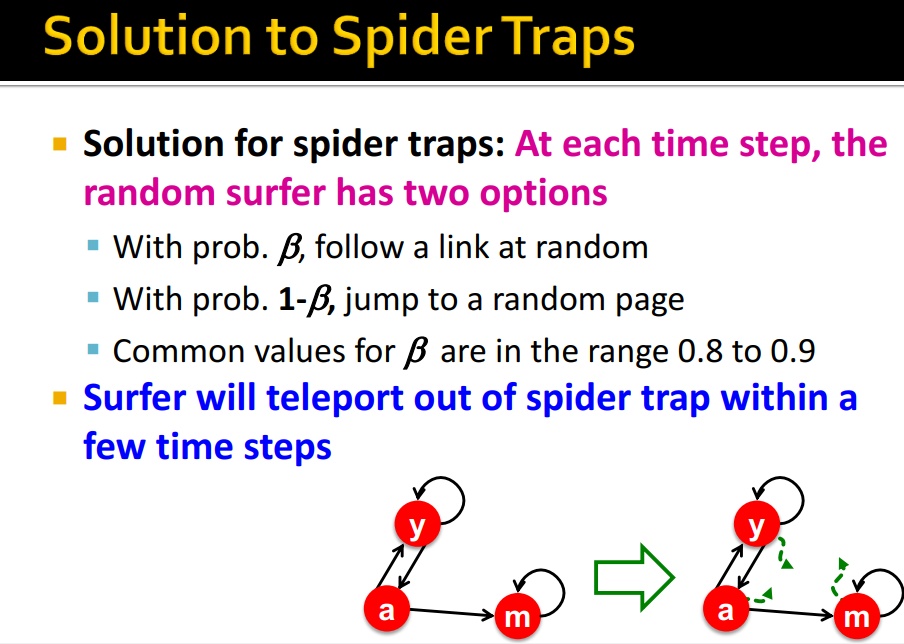
为什么 teleport 能够解决问题呢？

  • spider-trap 不是实际的问题，只是会导致我们求得值不准确
  • dead ends 才是问题，会导致列和不为 1，不满足我们的 assumption，所以需要调整 M

综合起来，就是 random teleports

  1. 概率 的可能继续随机走
  2. 概率 的可能跳转到其他随机页面

PageRank equation：[Brin-Page, 98]

**Google Matrix ** :

(平均跳转 5 次即可)