机器学习中如何处理不平衡数据
准确率高达 96.2% 的模型跑在真实数据上却可能完全无法使用。一个可能的原因是:你所使用的训练数据是不平衡数据集。本文介绍了解决不平衡类分类问题的多种方法。
假设老板让你创建一个模型——基于可用的各种测量手段来预测产品是否有缺陷。你使用自己喜欢的分类器在数据上进行训练后,准确率达到了 96.2%!
你的老板很惊讶,决定不再测试直接使用你的模型。几个星期后,他进入你的办公室,拍桌子告诉你你的模型完全没用,一个有缺陷的产品都没发现。
经过一番调查,你发现尽管你们公司的产品中大约有 3.8%的存在缺陷,但你的模型却总是回答「没有缺陷」,也因此准确率达到 96.2%。你之所以获得这种「naive」的结果,原因很可能是你使用的训练数据是不平衡数据集。
本文将介绍解决不平衡数据分类问题的多种方法。
首先我们将概述检测」naive behaviour」的不同评估指标;然后讨论重新处理数据集的多种方法,并展示这些方法可能会产生的误导;最后,我们将证明重新处理数据集大多数情况下是继续建模的最佳方式。
注:带(∞)符号的章节包含较多数学细节,可以跳过,不影响对本文的整体理解。此外,本文大部分内容考虑两个类的分类问题,但推理可以很容易地扩展到多类别的情况。
检测「naive behaviour」
我们先来看几种评估分类器的方法,以确保检测出「naive behaviour」。如前所述,准确率虽然是一个重要且不可忽视的指标,但却可能产生误导,因此应当谨慎使用,最好与其他指标一起使用。我们先看看还有哪些指标。
混淆矩阵、精度、召回率和 F1
在处理分类问题时,一个很好且很简单的指标是混淆矩阵(confusion matrix)。该指标可以很好地概述模型的运行情况。因此,它是任何分类模型评估的一个很好的起点。下图总结了从混淆矩阵中可以导出的大部分指标:
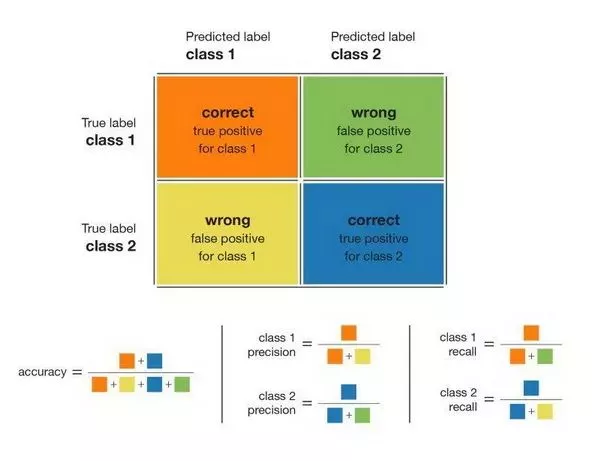
混淆矩阵以及可从中导出的指标。
让我们简单解释一下:所谓准确率(accuracy)就是正确预测的数量除以预测总数;类别精度(precision)表示当模型判断一个点属于该类的情况下,判断结果的可信程度。类别召回率(recall)表示模型能够检测到该类的比率。类别的 F1 分数是精度和召回率的调和平均值(F1 = 2×precision×recall / (precision + recall)),F1 能够将一个类的精度和召回率结合在同一个指标当中。
对于一个给定类,精度和召回率的不同组合如下:
-
高精度+高召回率:模型能够很好地检测该类;
-
高精度+低召回率:模型不能很好地检测该类,但是在它检测到这个类时,判断结果是高度可信的;
-
低精度+高召回率:模型能够很好地检测该类,但检测结果中也包含其他类的点;
-
低精度+低召回率:模型不能很好地检测该类。
我们举个例子,如下图所示,我们有 10000 个产品的混淆矩阵:
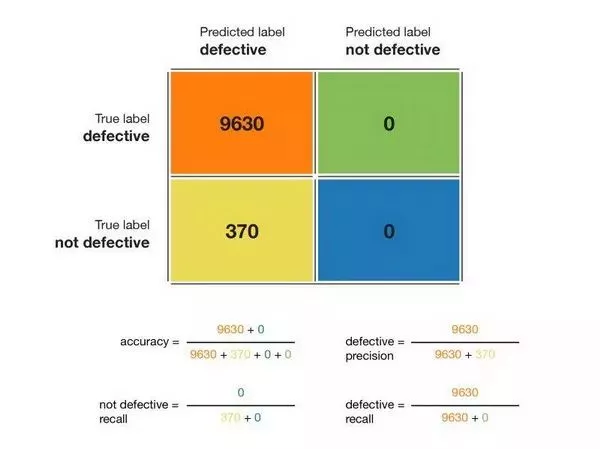
文章开头示例的混淆矩阵。注意「not defective」精度不可计算。
根据上图,准确率为 96.2%,无缺陷类的精度为 96.2%,有缺陷类的精度不可计算;无缺陷类的召回率为 1.0(这很好,所有无缺陷的产品都会被检测出来),有缺陷类的召回率是 0(这很糟糕,没有检测到有缺陷的产品)。因此我们可以得出结论,这个模型对有缺陷类是不友好的。有缺陷产品的 F1 分数不可计算,无缺陷产品的 F1 分数是 0.981。在这个例子中,如果我们查看了混淆矩阵,就会重新考虑我们的模型或目标,也就不会有前面的那种无用模型了。
ROC 和 AUROC
另外一个有趣的指标是ROC 曲线(Receiver Operating Characteristic),其定义和给定类相关(下文用 C 表示类别)。
假设对于给定点 x,我们的模型输出该点属于类别 C 的概率为:P(C | x)。基于这个概率,我们定义一个决策规则,即当且仅当 P(C | x)≥T 时,x 属于类别 C,其中 T 是定义决策规则的给定阈值。如果 T = 1,则仅当模型 100%可信时,才将该点标注为类别 C。如果 T = 0,则每个点都标注为类别 C。
阈值 T 从 0 到 1 之间的每个值都会生成一个点 (false positive, true positive),ROC 曲线就是当 T 从 1 变化到 0 所产生点的集合所描述的曲线。该曲线从点 (0,0) 开始,在点 (1,1) 处结束,且单调增加。好模型的 ROC 曲线会快速从 0 增加到 1(这意味着必须牺牲一点精度才能获得高召回率)。
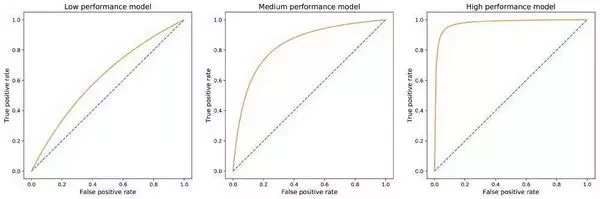
有效性不同的模型的 ROC 曲线图示。左侧模型必须牺牲很多精度才能获得高召回率;右侧模型非常有效,可以在保持高精度的同时达到高召回率。
基于 ROC 曲线,我们可以构建另一个更容易使用的指标来评估模型:AUROC(Area Under the ROC),即 ROC 曲线下面积。可以看出,AUROC 在最佳情况下将趋近于 1.0,而在最坏情况下降趋向于 0.5。同样,一个好的 AUROC 分数意味着我们评估的模型并没有为获得某个类(通常是少数类)的高召回率而牺牲很多精度。
究竟出了什么问题?
不平衡案例
在解决问题之前,我们要更好地理解问题。为此我们考虑一个非常简单的例子。假设我们有两个类:C0 和 C1,其中 C0 的点遵循均值为 0、方差为 4 的一维高斯分布;C1 的点遵循均值为 2 、方差为 1 的一维高斯分布。假设数据集中 90% 的点来自 C0,其余 10% 来自 C1。下图是包含 50 个点的数据集按照上述假设的理论分布情况:
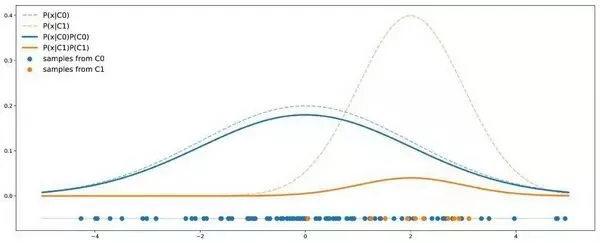
不平衡案例图示。虚线表示每个类的概率密度,实线加入了对数据比例的考量。
在这个例子中,我们可以看到 C0 的曲线总是在 C1 曲线之上,因此对于任意给定点,它出自 C0 类的概率总是大于出自 C1 类的概率。用贝叶斯公式来表示,即:
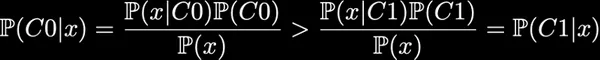
在这里我们可以清楚地看到先验概率的影响,以及它如何导致一个类比另一个类更容易发生的情况。这就意味着,即使从理论层面来看,只有当分类器每次判断结果都是 C0 时准确率才会最大。所以假如分类器的目标就是获得最大准确率,那么我们根本就不用训练,直接全部判为 C0 即可。
关于可分离性
在前面的例子中,我们可以观察到两个类似乎不能很好地分离开(彼此相距不远)。但是,数据不平衡不代表两个类无法很好地分离。例如,我们仍假设数据集中 C0、C1 的比例分别为 90% 和 10%;但 C0 遵循均值为 0 、方差为 4 的一维高斯分布、C1 遵循均值为 10 、方差为 1 的一维高斯分布。如下图所示:
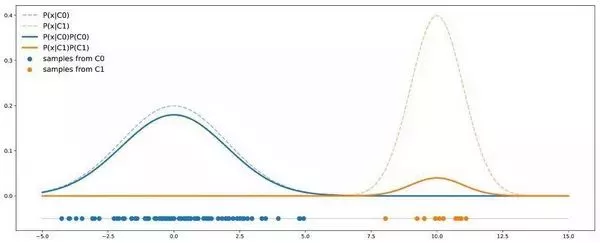
在这个例子中,如果均值差别足够大,即使不平衡类也可以分离开来。
在这里我们看到,与前一种情况相反,C0 曲线并不总是高于 C1 曲线,因此有些点出自 C1 类的概率就会高于出自 C0 的概率。在这种情况下,两个类分离得足够开,足以补偿不平衡,分类器不一定总是得到 C0 的结果。
理论最小误差概率
我们应当明白这一点,分类器具有理论意义上的最小误差概率。对于本文所讨论的单特征二分类分类器,用图表来看的话,理论最小误差概率是由两条曲线最小值下的面积给出的:
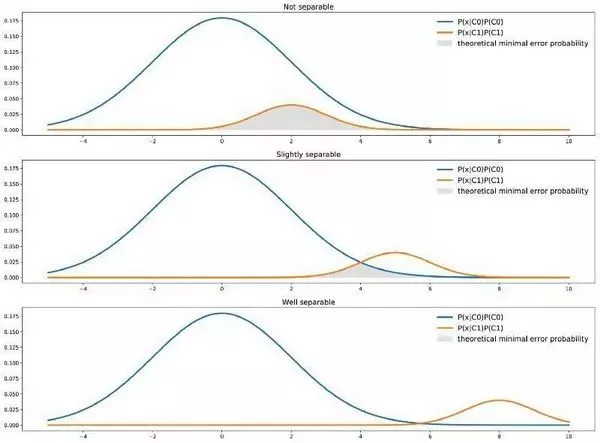
两个类在不同分离度下的理论最小误差。
我们可以用公式的形式来表示。实际上,从理论的角度来看,最好的分类器将从两个类中选择点 x 最有可能属于的类。这自然就意味着对于给定的点 x,最好的理论误差概率由这两个类可能性较小的一个给出,即
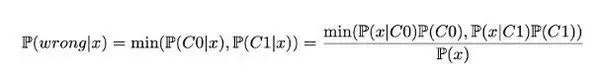
然后我们可以对全体进行积分,得到总误差概率:
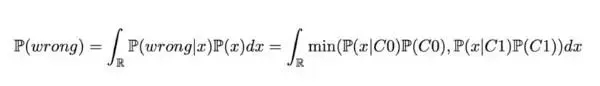
即上图中两条曲线最小值下区域的面积。
重新处理数据集并不总是解决方案
面对不平衡数据集,我们的第一个反应可能会认为这个数据没有代表现实。如果这是正确的,也就是说,实际数据应该是(或几乎是)平衡的,但由于我们采集数据时的方法问题造成数据存在比例偏差。因此我们必须尝试收集更具代表性的数据。
在接下来的两个小节里,我们将简单介绍一些常用于解决不平衡类以及处理数据集本身的方法,特别是我们将讨论欠采样(undersampling)、过采样(oversampling)、生成合成数据的风险及好处。
欠采样、过采样和生成合成数据
这三种方法通常在训练分类器之前使用以平衡数据集。简单来说:
-
欠采样:从样本较多的类中再抽取,仅保留这些样本点的一部分;
-
过采样:复制少数类中的一些点,以增加其基数;
-
生成合成数据:从少数类创建新的合成点,以增加其基数。
所有这些方法目的只有一个:重新平衡(部分或全部)数据集。但是我们应该重新平衡数据集来获得数据量相同的两个类吗?或者样本较多的类应该保持最大的代表性吗?如果是这样,我们应以什么样的比例来重新平衡呢?
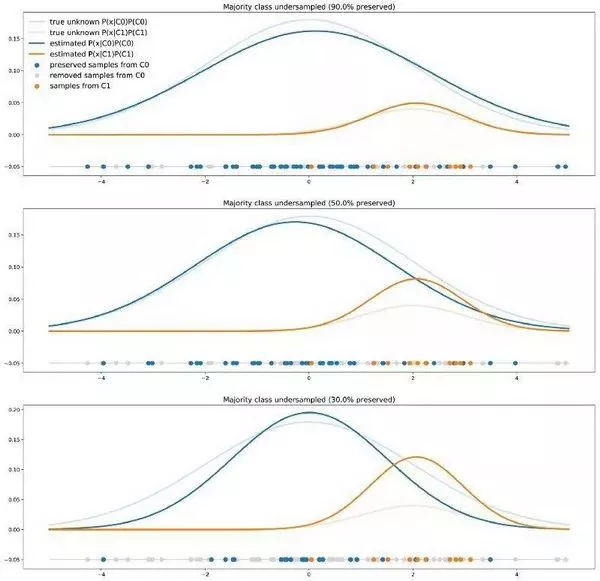
不同程度的多数类欠采样对模型决策的影响。
当使用重采样方法(例如从 C0 获得的数据多于从 C1 获得的数据)时,我们在训练过程向分类器显示了两个类的错误比例。以这种方式学得的分类器在未来实际测试数据上得到的准确率甚至比在未改变数据集上训练的分类器准确率还低。实际上,类的真实比例对于分类新的点非常重要,而这一信息在重新采样数据集时被丢失了。
因此,即使不完全拒绝这些方法,我们也应当谨慎使用它们:有目的地选择新的比例可以导出一些相关的方法(下节将会讲),但如果没有进一步考虑问题的实质而只是将类进行重新平衡,那么这个过程可能毫无意义。总结来讲,当我们采用重采样的方法修改数据集时,我们正在改变事实,因此需要小心并记住这对分类器输出结果意味着什么。
添加额外特征
重采样数据集(修改类比例)是好是坏取决于分类器的目的。如果两个类是不平衡、不可分离的,且我们的目标是获得最大准确率,那么我们获得的分类器只会将数据点分到一个类中;不过这不是问题,而只是一个事实:针对这些变量,已经没有其他更好的选择了。
除了重采样外,我们还可以在数据集中添加一个或多个其他特征,使数据集更加丰富,这样我们可能获得更好的准确率结果。回到刚才的例子(两个类无法很好地分离开来),我们附加一个新的特征帮助分离两个类,如下图所示:
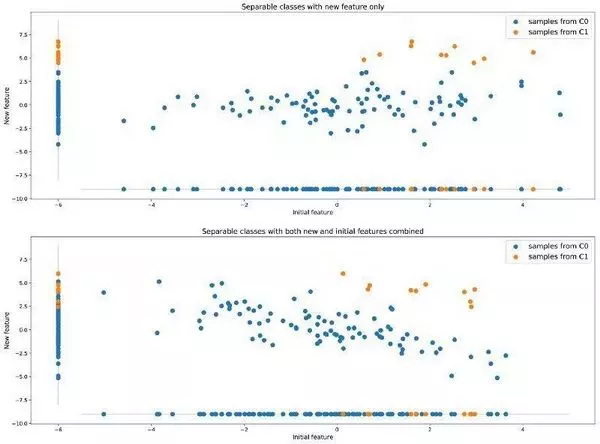
寻找附加特征可以将原本不能分离的类分离开。
与前一小节提到的重采样的方法相比,这种方法会使用更多来自现实的信息丰富数据,而不是改变数据的现实性。
重新解决问题更好
到目前为止,结论似乎令人失望:如果要求数据集代表真实数据而我们又无法获得任何额外特征,这时候如果我们以最佳准确率来评判分类器,那么我们得到的就是一个「naive behaviour」(判断结果总是同一个类),这时候我们只好将之作为事实来接受。
但如果我们对这样的结果不满意呢?这就意味着,事实上我们的问题并没有得到很好的表示(否则我们应当可以接受模型结果),因此我们应该重新解决我们的问题,从而获得期望结果。我们来看一个例子。
基于成本的分类
结果不好的根本原因在于目标函数没有得到很好的定义。截至此时,我们一直假设分类器具备高准确率,同时假设两类错误(「假阳性」和「假阴性」)具有相同的成本(cost)。在我们的例子中,这意味着真实标签为 C1、预测结果为 C0 与真实标签为 C0、预测结果为 C1 一样糟糕,错误是对称的。然而实际情况往往不是这样。
让我们考虑本文第一个例子,关于有缺陷(C1)和无缺陷(C0)产品。可以想象,对公司而言,没有检测到有缺陷的产品的代价远远大于将无缺陷的产品标注为有缺陷产品(如客户服务成本、法律审判成本等)。因此在真实案例中,错误的代价是不对称的。
我们再更具体地考虑,假设:
-
当真实标签为 C1 而预测为 C0 时的成本为 P01
-
当真实标签为 C0 而预测为 C1 时的成本为 P10
-
其中 P01 和 P10 满足:0
接下来,我们可以重新定义目标函数:不再以最佳准确率为目标,而是寻找较低的预测成本。
理论最小成本 (∞)
从理论的角度来看,我们并不想最小化前文定义的误差概率,而是最小化期望预测成本:

其中 C(.) 定义分类器函数。因此,如果我们想要最小化期望预测成本,理论最佳分类器 C(.) 最小化
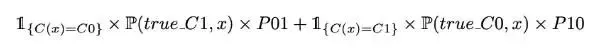
或者等价地,除以 x 的密度,C(.) 最小化
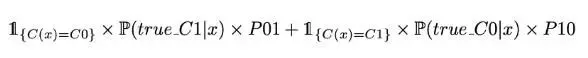
有了这个目标函数,从理论的角度来看,最好的分类器应该是这样的:
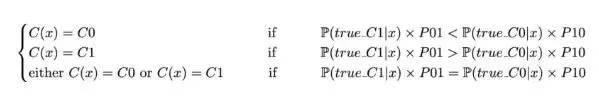
注意:当成本相等时,我们就恢复了「经典」分类器的表达式(只考虑准确率)。
概率阈值
在分类器中考虑成本的第一种可行方法是在训练后进行,也即按照基本的方法训练分类器,输出如下概率:
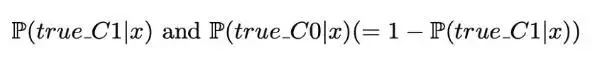
这里没有考虑任何成本。然后,如果满足下述条件
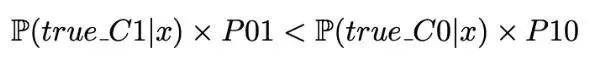
则预测类为 C0,否则为 C1。
这里,只要输出给定点的每个类的概率,使用哪个分类器并不重要。在我们的例子中,我们可以在数据上拟合贝叶斯分类器,然后对获得的概率重新加权,根据成本误差来调整分类器。
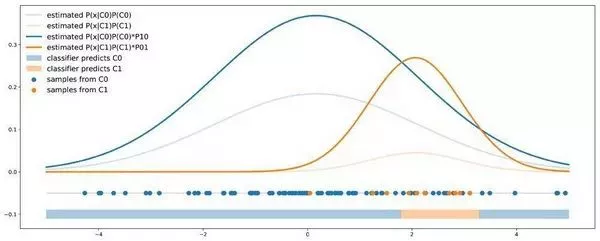
概率阈值方法:输出概率被重新加权,使得在最终决策规则中考虑成本。
类重新加权
类重新加权(class reweight),即在分类器训练期间直接考虑成本误差的不对称性,这使每个类的输出概率都嵌入成本误差信息。然后这个概率将用于定义具有 0.5 阈值的分类规则。
对于某些模型(例如神经网络分类器),我们可以在训练期间通过调整目标函数来考虑成本。我们仍然希望分类器输出
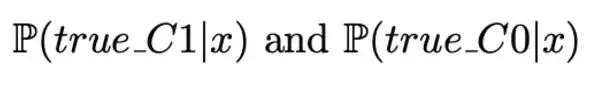
但是这次的训练将使以下的成本函数最小化
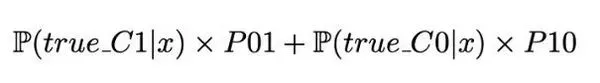
对于一些其他模型(例如贝叶斯分类器),我们可以使用重采样方法来偏置类的比例,以便在类比例内输入成本误差信息。如果考虑成本 P01 和 P10(如 P01> P10),我们可以:
- 对少数类按照 P01 / P10 的比例进行过采样(少数类的基数乘以
- 原文作者:知识铺
- 原文链接:https://index.zshipu.com/geek/post/%E4%BA%92%E8%81%94%E7%BD%91/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0%E4%B8%AD%E5%A6%82%E4%BD%95%E5%A4%84%E7%90%86%E4%B8%8D%E5%B9%B3%E8%A1%A1%E6%95%B0%E6%8D%AE/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


