机器学习与数据科学决策树指南
还在为如何抉择而感到纠结吗?快采用决策树(Decision Tree)算法帮你做出决定吧。决策树是一类非常强大的机器学习模型,具有高度可解释的同时,在许多任务中也有很高的精度。决策树在机器学习模型领域的特殊之处在于其信息表示的很清楚,而不像一些机器学习方法是个黑匣子,这是因为决策树通过训练学到的“知识”直接形成层次结构,该结构以这样的方式保存和显示学到的知识,即使是非专业人士也可以容易地弄明白。

现实生活中的决策树
在现实生活中,我们常常用过类似于决策树的方式来决定自己的生活。例如,决定周末安排什么样的活动。采取怎样的活动可能取决于一些因素,比如是否愿意和朋友一起出去或独自度过周末、周末的天气如何等。假设就这两个因素影响你做出决定的话,如果天气晴朗,并且你的朋友可以一起参与,那么你可能想踢足球。如果是下雨天,可能会一起去看电影。如果朋友有事无法参加,那么无论天气如何,可能会去看会书、玩会电子游戏。
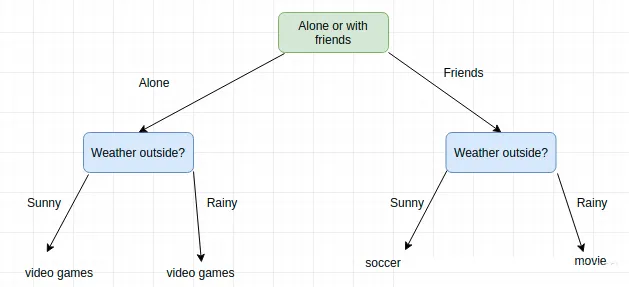
这就是现实中的一个明显的决策树例子,上述已经构建了一个树来模拟一组顺序的、层次化的决策,最终得到一个结果。这里,为了保持树的小巧,还选择了相当“高级”的决策。
例如,如果为天气设置了许多可能的选项,例如晴天(25度)、下雨(25度)、晴天(26度)、下雨(26度)、晴天(27度)…… 等等,这样会使得树尺寸会很大,这种精确的温度对于最后做出的决策没有太相关的关系,因为只是想知道是外界是否下雨,根据下雨的情况决定是否外出,而温度的高低对其影响很小。当然,极寒极热天气还是在家比较舒服。
机器学习中的决策树的概念和上面的思想是相同的,需要构建一个具有一组分层决策的树,最终给出决策结果,即分类或回归预测。尽可能使得决策树尺寸较小,同时要实现高分类/回归准确性。
机器学习中的决策树
决策树模型的构建一般分为两个步骤:归纳(induction)和修剪(pruning)。归纳是实际构建树的步骤,即根据我们的数据设置所有的分层决策边界。但由于训练决策树的性质,树模型可能容易出现严重的过拟合现象。这个时候就需要采用修剪处理,修剪就是从决策树中删除不必要的分支结构的过程,有效地降低了对抗过拟合的复杂性,并使其更容易解释。
归纳|Induction
从高层次来看,决策树归纳需要经过4个主要步骤:
-
训练数据集应具有一些特征变量、分类或回归输出;
-
确定数据集中的“最佳特征”以分割数据;
-
将数据拆分为包含此最佳特征的可能值的子集,这种分裂基本上定义了树上的节点,即每个节点是基于数据中的某个特征的分裂点;
-
使用从步骤3创建的数据子集递归地生成新的树节点,保持分裂直到达到一个优化点,在该点已经通过某种度量优化了最大精度,同时最小化了分裂/节点的数量。
第1步很简单,只需好好分析数据集。对于步骤2,通常使用贪婪算法来选择要使用的特征和特定分割,以最小化代价函数。构建决策树时执行的拆分相当于划分特征空间。我们将迭代地尝试不同的分割点,最后选择成本最低的分割点。也可以只在数据集中的值范围内进行拆分,这将使得我们免于浪费计算来测试那些表现差的分裂点。
对于回归树,可以使用简单的平方误差作为模型的代价函数:
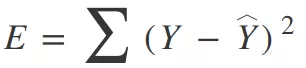
其中,Y是期望输出,Y-hat是预测值,对数据集中的所有样本求和以获得总误差。对于分类,使用的是基尼指数函数(Gini Index Function):
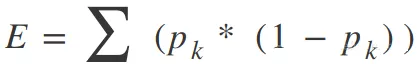
其中pk是特定预测节点中第k类的训练实例样本的比例。理想情况下, 节点的错误值应为零,这意味着每个拆分输出的类正是我们想要的,一旦到达那个特定的决策节点,无论处于决策边界的这一边还是另一边,其输出也确定好了。
在数据集中具有单个分类的概念被称为信息增益。以下是举例:
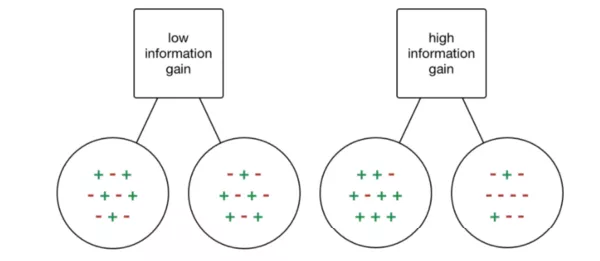
如果选择了某种划分,其中每个输出根据输入数据混合类别,这种情况实际上根本没有获得任何信息; 另一方面,如果采取的分割对于每个输出的类的正确率都很高,那么已经获得 了在具体特征变量上以特定方式分割的信息。
之后是对树模型进行分裂,直到树有数千个分支,但这不是一个好主意!这样得到的决策树将是巨大的、缓慢的,并且会过拟合训练数据集。因此,需要设置一些预定义的停止标准来停止树的构造。
最常见的停止方法是对分配给每个叶节点的训练样本的数量使用最小数量。如果计数小于某个最小值,则不接受拆分,并将该节点作为最终叶节点。如果所有的叶子节点都成为最终节点,则训练停止。较小的最小数量将提供更精细的分割和信息,但也容易过拟合训练数据。因此,最小数量的取值通常基于数据集设置,具体取决于每个类中预计有多少个示例样本。
修剪|Pruning
由于训练决策树的性质,可能容易会出现严重的过拟合现象。为每个节点设置最小实例数的正确值可能具有挑战性。大多数情况下,可能只是希望做出合适的决定,而无需最优的决定。因此,无需使得最小值非常小获得非常复杂的树,且有很多分裂是多余的,并没有提高模型的准确性。
树修剪是一种利用修剪树中不必要的分裂的技术。从上层开始,修剪将树的一部分从严格的决策边界压缩为更平滑、更通用的树,从而有效地降低树的复杂性。决策树的复杂性定义为树中的分裂数。
一种简单而高效的修剪方法是遍历树中的每个节点,并评估将其移除后其代价函数上的效果。如果移除后,代价函数变化不大,那就修剪掉该节点。
实例实践
使用Scikit Lear中内置的函数来实现分类和回归的决策树是非常容易的。首先加载数据集并初始化决策树以进行分类。
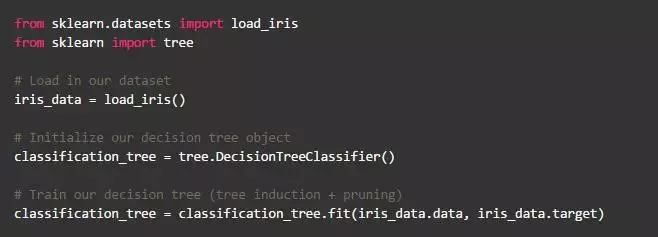
Scikit.还允许使用graphviz库可视化构建的树,它附带了一些选项,这些选项将有助于可视化决策节点,并将模型学到的内容进行分割,下面根据特征名称对节点进行着色,并显示每个节点的类和特征信息:
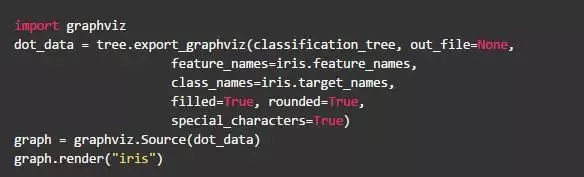
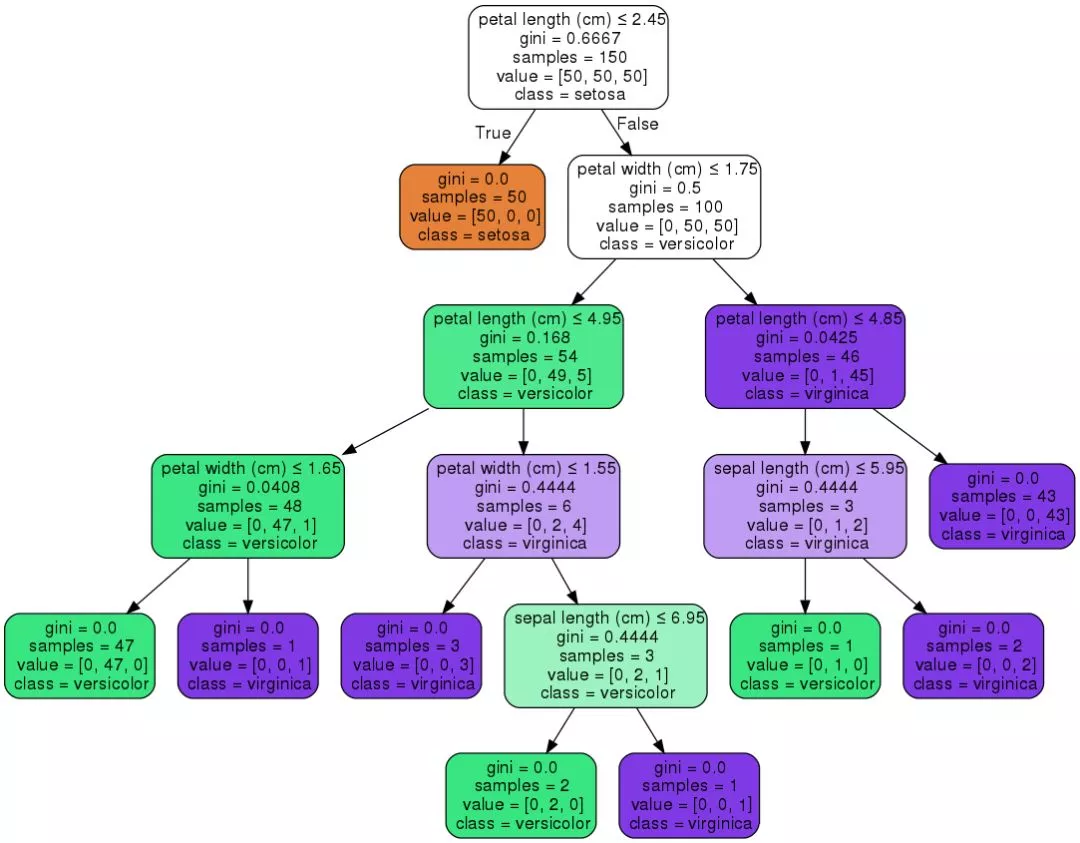
也可以在Scikit Learn中为决策树模型设置几个参数。以下是一些有趣的尝试以获得更好的结果:
-
max_depth:树的最大深度,类似于深度神经网络中的最大层数。较浅会使得模型更快但不准确;更深的模型可能会使得准确性更高,但过拟合的风险也增大,且运行很慢;
-
min_samples_split: 拆分节点所需的最小样本数, 将其设置为合适的值将有助于减轻过拟合;
-
max_features:查找最佳拆分时要考虑的特征数,更高可能意味着更好的结果,但训练也需要更长的时间;
-
min_impurity_split:树生长早期停止的阈值,如果节点的杂质高于阈值,则该节�
- 原文作者:知识铺
- 原文链接:https://index.zshipu.com/geek/post/%E4%BA%92%E8%81%94%E7%BD%91/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0%E4%B8%8E%E6%95%B0%E6%8D%AE%E7%A7%91%E5%AD%A6%E5%86%B3%E7%AD%96%E6%A0%91%E6%8C%87%E5%8D%97/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


