揭开深度推荐系统模型之谜
今天我们着手来彻底解决一个许久以来悬而未决的问题，也至少有十几位专栏读者通过留言和私信的方式询问我这个问题，这个问题就是 YouTube深度学习推荐系统中模型serving的问题。
不了解YouTube深度学习推荐系统的同学可以回顾一下我之前的两篇专栏文章，以及YouTube的论文原文：
- 王喆：重读Youtube深度学习推荐系统论文，字字珠玑，惊为神文
- 王喆：YouTube深度学习推荐系统的十大工程问题
- [Youtube] Deep Neural Networks for YouTube Recommendations (Youtube 2016)
这里我们再详细陈述一下这个问题：
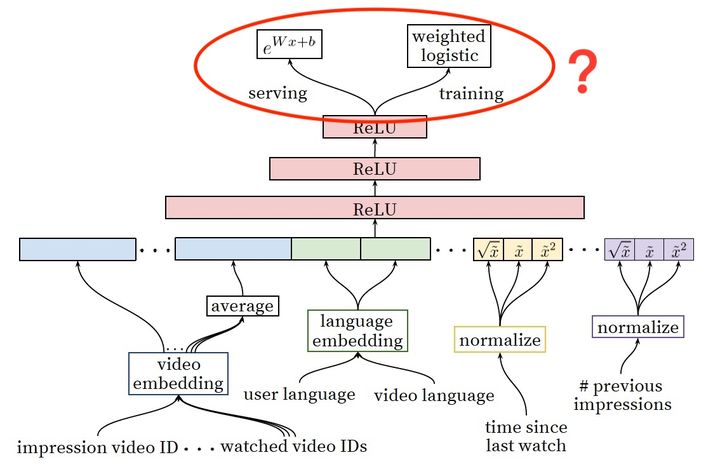
YouTube深度学习推荐系统中Ranking Model的架构图
上图是YouTube推荐系统排序模型（Ranking Model）的架构图，我们不再重复讲解模型的细节，而是把关注的焦点放在最后的输出层：
**为什么Ranking Model采用了weighted logistic regression作为输出层？在模型serving过程中又为何没有采用sigmoid函数预测正样本的probability，而是使用
这一指数形式预测用户观看时长？**
对于传统的深度学习架构，输出层往往采用LR或者Softmax，在线上预测过程中，也是原封不动的照搬LR或者softmax的经典形式来计算点击率（广义地说，应该是正样本概率）。
而YouTube这一模型的神奇之处在于，输出层没有使用LR，而是采用了Weighted LR，模型serving没有采用sigmoid函数的形式，而是使用了
这一指数形式。按照原文说法，这样做预测的就是用户观看时长？？没有任何其他表情能像这位小哥一样表达我初读论文的感受。。What？？？
搞清楚这件事情并不是一件容易的事情，我们要从逻辑回归的 本质意义 上开始。
几乎所有算法工程师的第一堂课就是逻辑回归，也肯定知道逻辑回归的数学形式就是一个线性回归套sigmoid函数：
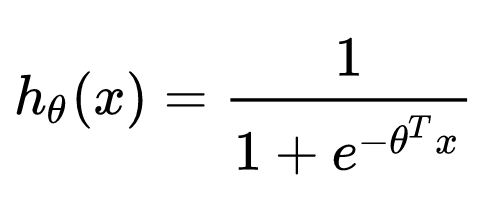
逻辑回归的数学形式
但为什么选择sigmoid函数？难道仅仅是sigmoid函数能把值域映射到0-1之间，符合概率的物理意义这么简单吗？
答案显然不会这么肤浅。
为解释这个问题，首先我们需要定义一个新的变量—— Odds，中文可以叫 发生比 或者 机会比。
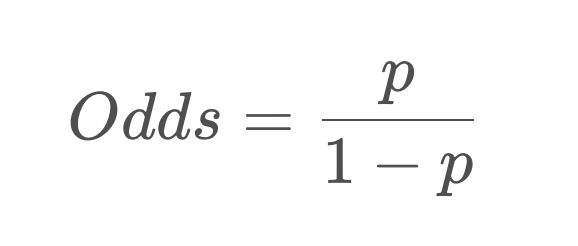
Odds的定义
假设一件事情发生的概率是p，那么 Odds就是一件事情发生和不发生的比值。
如果对Odds取自然对数，再让ln(Odds)等于一个线性回归函数，那么就得到了下面的等式。
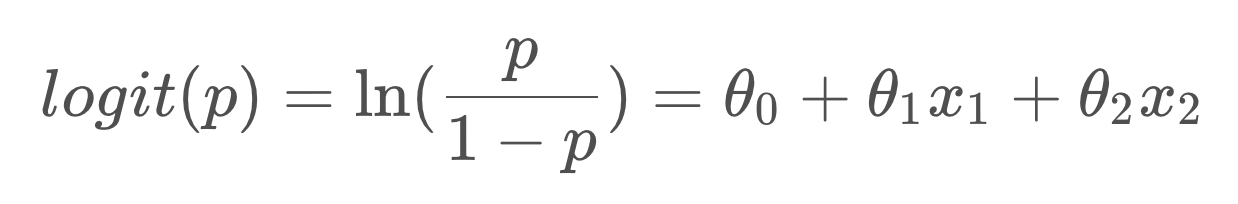
其中ln(p/(1-p))就是大名鼎鼎的 logit函数，logistics regression又名logit regression，上面的式子就是逻辑回归的由来。我们再做进一步运算，就可以转变成我们熟悉的逻辑回归的形式：
