推荐系统协同过滤推荐算法
来源: 算法研习社
相信大家对推荐系统已经很熟悉了,它通过分析用户的历史行为,挖掘用户的兴趣爱好,预测并推荐给用户其接下来有可能感兴趣的事物,例如商品推荐、音乐推荐、新闻以及最近很火的短视频推荐等等。
协同过滤推荐 作为最为主流与经典的技术之一,它是基于这样的假设: 用户如果在过去对某些项目产生过兴趣,那么将来他很可能依然对其保持热忱。 协同过滤技术又可依据是否采用了机器学习思想建模进一步划分为基于内存的协同过滤(Memory-based CF)与基于模型的协同过滤技术(Model-based CF)。
本文旨在对经典的协同过滤推荐算法进行总结,并通过 Python 代码实现深入理解其算法原理。
目录:
基于内存的协同过滤推荐
- userCF
- itemCF
基于模型的协同过滤推荐
- 经典 SVD
- FunkSVD
- BiasSVD
- FISM
- SVD++
基于内存的协同过滤推荐
基于内存的协同过滤算法是推荐系统中最基本的算法,也叫做基于邻域的协同过滤,该算法不仅在学术界得到了深入研究,而且在业界得到了广泛应用。基于邻域的算法分为两大类,一类是基于用户的协同过滤算法,另一类是基于物品的协同过滤算法。
为了描述简便,下面的算法讲解都是基于我们常见的 topN 推荐场景,而不是评分预测场景。在 topN 场景中,我们只关注用户对物品是否具有行为,而不在乎分数。
数据集采用 MovieLens 中等大小的数据集,包含 6000 多用户对 4000 多部电影的 100 万条评分(1~5 分)。
数据集下载地址: http://files.grouplens.org/datasets/movielens/
输入数据处理为下面的格式:data => {user_id : { item_id :score}}
基于用户的协同过滤(User CF)
基于用户的协同过滤推荐,一句话概括就是,给用户 A 推荐 与其兴趣相似的朋友们喜欢而用户 A 还没听说过的 物品。
该算法主要包括两个步骤:
(1) 找到和目标用户兴趣相似的用户集合。
(2) 找到这个集合中用户喜欢的,且目标用户没有听说过的物品推荐给目标用户。
1.计算用户相似度
给定用户 u 和用户 v,令 N(u)表示用户 u 曾经有过反馈的物品集合,令 N(v)为用户 v 曾经有过反馈的物品集合。
通过余弦相似度计算用户 u 和 v 的相似度:
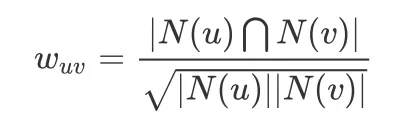
代码实现:
def UserSimilarity(train):
W = dict()
for u in train.keys():
for v in train.keys():
if u == v:
continue
W[u][v] = len(train[u] & train[v])
W[u][v] /= np.sqrt(len(train[u]) * len(train[v]) * 1.0)
return W
如果实际应用中用户数过多,上面计算方式是计算每两个用户的相似度,这样很多没必要的时间都浪费了。因此,可以先建立物品到用户的倒排表 item_users,对于每个物品都保存对该物品产生过行为的用户,然后遍历每个 item 的 users。
def UserSimilarity(train):
# 建立 item -> users table
item_users = dict()
for u, items in train.items():
for i in items.keys():
if i not in item_users:
item_users[i] = set()
item_users[i].add(u)
# 记录每个用户反馈过的物品数
N = dict()
# 记录每两个用户共同反馈过的物品数
C = dict()
for i, users in item_users.items():
for u in users:
N[u] += 1
for v in users:
if u == v:
continue
C[u][v] += 1
# 计算用户相似度权重矩阵
W = dict()
for u, related_users in C.items():
for v, cuv in related_users.items():
W[u][v] = cuv / np.sqrt(N[u] * N[v])
return W
2.基于相似用户推荐物品
得到用户之间的兴趣相似度后,UserCF 算法会给用户推荐和他兴趣最相似的 K 个用户喜欢过但该用户还没见过的物品。如下的公式度量了 UserCF 算法中用户 u 对物品 i 的感兴趣程度:
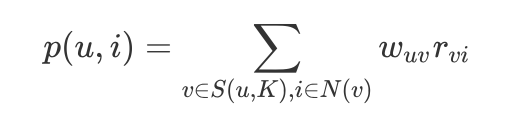
其中,S(u, K)包含和用户 u 兴趣最接近的 K 个用户,N(v)是用户 v 喜欢的物品集合,wuv 是用户 u 和用户 v 的兴趣相似度,r_{vi} 代表用户 v 对物品 i 的兴趣,因为使用的是单一行为的隐反馈数 据,所以所有的r_{vi} =1。
def Recommend(user_id, train, W, K):
rank_rs = dict()
interacted_items = train[user_id]
for v, wuv in sorted(W[user_id].items(), key=lambda x:x[1], reverse=True)[0:K]:
for i, rvi in train[v].items:
if i in interacted_items:
# 过滤掉该用户之前反馈过的物品
continue
rank_rs[i] += wuv * rvi
return rank_rs
基于物品的协同过滤(Item CF)
基于物品的协同过滤(item-based collaborative filtering)算法是目前业界应用最多的算法。Item CF 认为,物品 A 和物品 B 具有很大的相似度是因为喜欢物品 A 的用户大都也喜欢物品 B。就好比大家熟悉的“看了又看”功能,图书网站给用户推荐《天龙八部》可以解释为该用户之前喜欢《射雕英雄传》,而这两本书被很多人共同喜欢过。
基于物品的协同过滤算法主要分为两步。
(1) 计算物品之间的相似度。
(2) 根据物品的相似度和该用户的历史行为给用户生成推荐列表。
1.计算物品相似度
基于余弦相似度,可以计算物品 i 和 j 直接的相似度:
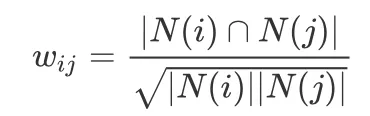
其中,N(i)表示喜欢物品 i 的用户集合,上式分母表示同时喜欢物品 i 和 j 的用户数。
def ItemSimilarity(train):
# 记录每个物品被反馈过的用户数
N = dict()
# 记录共同喜欢两个物品的用户数
C = dict()
for u, items in train.items():
for i in items:
N[i] += 1
for j in items:
if i == j:
continue
C[i][j] += 1
# 计算物品 i 和 j 的相似度矩阵
W = dict()
for i, related_items in C.items():
for j, cij in related_items.items():
W[i][j] = cij / np.sqrt(N[i] * N[j])
return W
2.基于相似用户推荐物品
在得到物品之间的相似度后,ItemCF 通过如下公式计算用户 u 对一个物品 j 的兴趣:
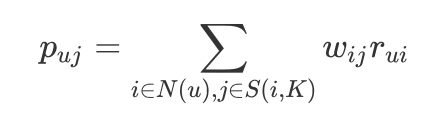
这里 N(u)是用户喜欢的物品的集合,S(i,K)是和物品 i 最相似的 K 个物品的集合,wij 是物品 j 和 i 的相似度,r_{ui} 是用户 u 对物品 i 的兴趣。
代码实现:
def Recommendation(train, user_id, W, K):
rank_rs = dict()
u_items = train[user_id]
for i, rui in u_items.items():
for j, wij in sorted(W[i].items(), key=lambda x: x[1], reverse=True)[0:K]:
if j in u_items:
continue
rank_rs[j] += rui * wij
return rank_rs
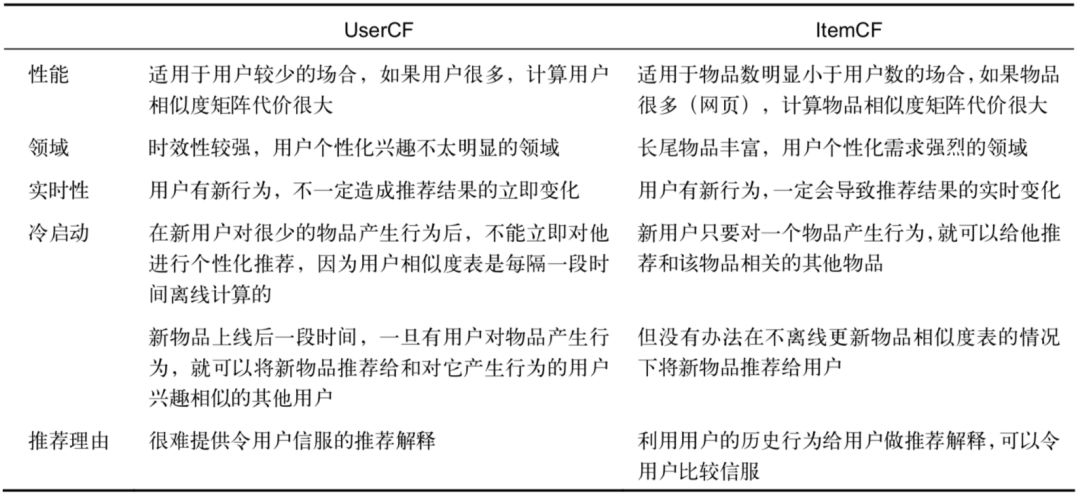
UserCF 和 Item CF 比较
- UserCF 给用户推荐那些和他有共同兴趣爱好的用户喜欢的物品,而 ItemCF 给用户推荐那些和他之前喜欢的物品类似的物品。
- UserCF 的推荐结果着重于反映和用户兴趣相似的小群体的热点,而 ItemCF 的推荐结果着重于维系用户的历史兴趣。
- UserCF 的推荐注重社会化,反映了用户所在的小型兴趣群体中物品的热门程度,而 ItemCF 的推荐更加个性化,反映了用户自己的兴趣传承。
- 从技术上考虑,UserCF 需要维护一个用户相似度的矩阵,而 ItemCF 需要维护一个物品相似度矩阵。
- 从存储的角度说,如果用户很多,那么维护用户兴趣相似度矩阵需要很大的空间, 同理,如果物品很多,那么维护物品相似度矩阵代价较大。
基于模型的协同过滤推荐
在经典的推荐算法中,除了基于邻域的 ItemCF 和 UserCF,提的最多的就是隐语义模型和矩阵分解模型。其实,这两个名词说的是一回事,就是如何通过降维的方法将评分矩阵补全。
若 R[u][i]表示用户 u 对物品 i 的评分,由于用户不会对所有的物品评分,所以真实的 R 矩阵是非常稀疏的,推荐算法要做的就是将这些缺失值补全,预测用户对未反馈过物品的评分,继而对高分物品进行推荐。
经典 SVD
最经典的基于矩阵分解的推荐技术是 SVD(奇异值)分解。
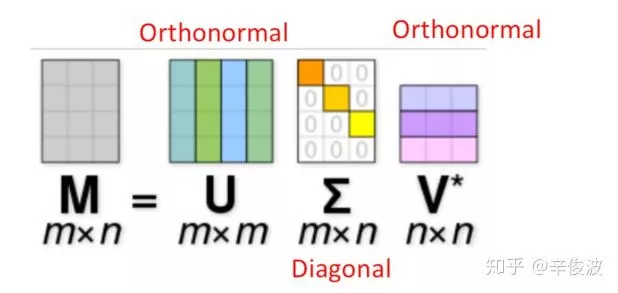
上图左侧 M=m*n 表示用户评分矩阵,m 矩阵的行表示用户数,n 矩阵的列表示 item 数,在大多数推荐系统中 m 和 n 规模都比较大,右侧三个矩阵依次是左奇异矩阵、奇异值矩阵和右奇异矩阵。如果只取前 k 个最大的奇异值组成对角矩阵 \sum_{k \times k} ,并且找到这 k 个奇异值中每个值在 U、V 矩阵中对应的列和行 U_{m\times k},V^T_{k \times t},得到 、,从而可以得到一个降维后的评分矩阵:
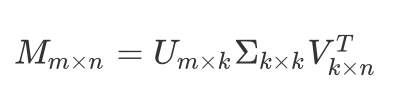
其中, M (u, i) 就是用户 u 对物品 i 评分的预测值,即完成了填空的任务。
一般来说,SVD 求解可以分为三步:
(1) 对 M 矩阵的 missing data 进行填充,整体均值、用户均值、物品均值或 0
(2) 求解 SVD 问题,得到 U 矩阵和 V 矩阵
(3) 利用 U 和 V 矩阵的低秩 k 维矩阵来估计 M
对于第二步中的 SVD 求解问题,等价于以下的最优化问题:
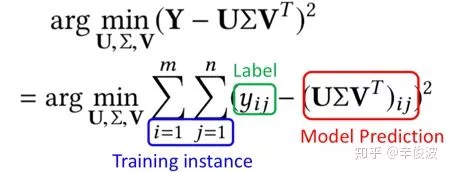
其中 y_{ij} 为用户 i 对物品 j 的真实评分,也就是 label, U 和 V 为模型预估值,求解矩阵 U 和 V 的过程就是最小化用户真实评分矩阵和预测矩阵误差的过程。
这种 SVD 求解方法存在以下问题:
(1) missing data(在数据集占比超过 95%)和 observe data 权重一样
(2) 最小化过程没有正则化(只有最小方差),容易产生过拟合
(3)计算复杂度很高,特别是在稠密的大规模矩阵上更是非常慢。
因此,一般来说针对原始的 SVD 方法会有很多改进方法。
FunkSVD
2006 年 Netflix Prize 开始后,Simon Funk 在博客上公布了一个算法(称为 Funk-SVD),解决了传统 SVD 的几个缺点。Simon Funk 提出的矩阵分解方法后来被 Netflix Prize 的冠军称为 Latent Factor Model(简称为 LFM),即隐语义模型。FunkSVD,将矩阵 M 分解为了 2 个 低秩 的 user,item 矩阵,

核心思想可以分成两步:
(1)将用户 u 对物品 i 的打分分解成用户的隐向量 vu,以及物品的隐向量 vi
(2)用户 u 和物品 i 的向量点积(inner product)得到的 value,可以用来代表用户 u 对物品 i 的喜好程度,分数越高代表该 item 推荐给用户的概率就越大
同时,FunkSVD 模型引入了 L2 正则来解决过拟合问题
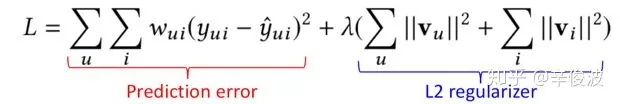
可以采用随机梯度下降法优化求解。
BiasSVD
实际情况下,一个评分系统有些固有属性和用户物品无关,而用户也有些属性和物品无关,物品也有些属性和用户无关。因此,Netflix Prize 中提出了另一种 LFM,其预测公式如下:
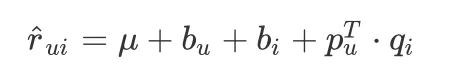
这个预测公式中加入了 3 项 \
- 原文作者:知识铺
- 原文链接:https://index.zshipu.com/geek/post/%E4%BA%92%E8%81%94%E7%BD%91/%E6%8E%A8%E8%8D%90%E7%B3%BB%E7%BB%9F%E5%8D%8F%E5%90%8C%E8%BF%87%E6%BB%A4%E6%8E%A8%E8%8D%90%E7%AE%97%E6%B3%95/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


