大家好，我是 为人造的智能操碎了心 的智能禅师。

最近很多读者问本禅师：

转行机器学习需要注意哪些事情呢？

我想学习机器学习，需要学习哪些知识呢？

机器学习如何避免走弯路呢？

本禅师表示非常理解大家的需求。

人工智能（其实本禅师认为目前看来翻译成人造智能可能更直白一点）毫无疑问，已经是科技趋势，却又是门槛相对较高、对学习者要求非常高的一门科学。

说起对机器学习所需要的基础知识掌握程度，一个有经验的开发者可能并不比刚开始接触机器学习的学生多。

机器学习有哪些关键要素？需要掌握什么语言？如何理解机器是怎么学习的？… 接下来，我们听听人工智能头条特约作者李烨，讲讲她开始学习机器学习的经验。

讲讲她踩过的那xiiieeeee坑们，以及如何从一个摸着石头过河的 机器学习的新手，逐步成为老司机的。

李烨，高级软件工程师，现就职于微软（Microsoft），曾在易安信（EMC）和太阳微系统（Sun Microsystems）任软件工程师。先后参与聊天机器人、大数据分析平台等项目的开发。

全文大约1500字。读完可能需要下面这首歌的时间

👇

The  Robot  Who  Lost  Its  HeadBuckethead - March  of  The  Slunks

学习“机器学习”这件事，我走过很长的一段弯路

有一些心得、体会和方法，在此和大家分享。

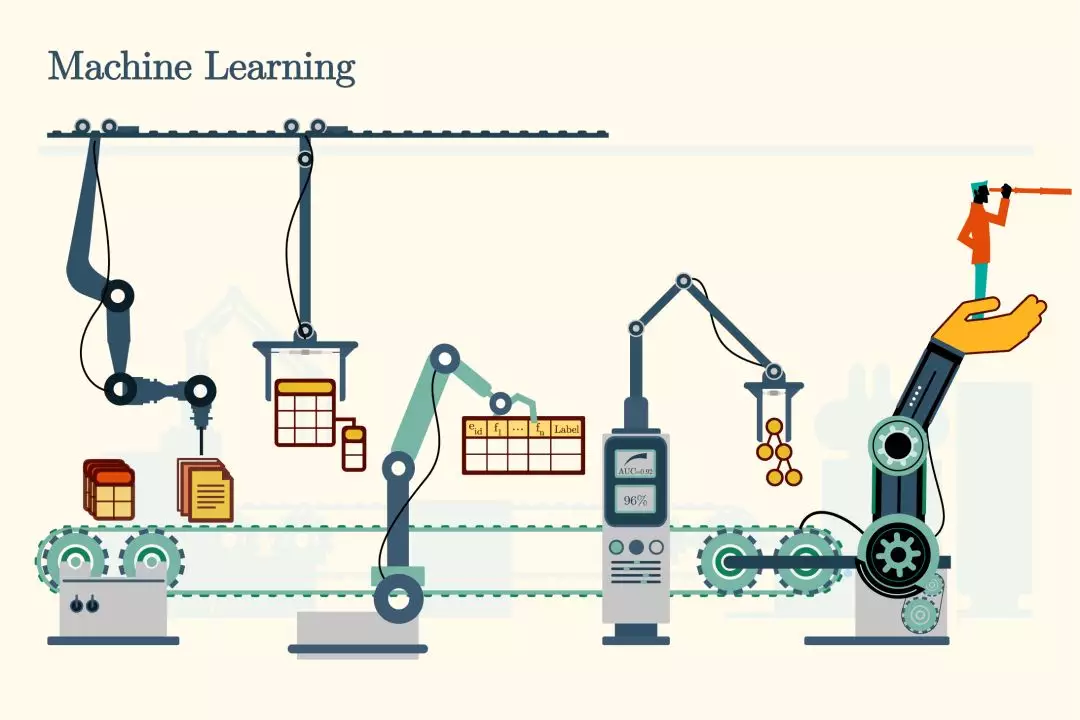
以模型为驱动，了解“机器学习”的本质

本课力图引导大家以模型为驱动，进行学习。

我选择了几种经典模型（例如：线性回归，逻辑回归，决策树，支持向量机，条件随机场，K 均值等），作为入门的进阶。

初次学习模型，不必贪多。但就这些选定的模型，一定要搞清楚其问题域、模型函数、目标函数、训练算法……潜入到数学公式推导的层面，对每一步的公式变换和对应物理意义有所理解，然后再去实践。

这一个个的模型，就是机器学习的“肌肉”，我们要通过观察学习这一块块肌肉，以其为载体来了解机器学习的核心——将事物转化为数值，将关系、变换转化为运算——以事实（数据）为依据，以规章（算法）为准绳，通过计算来掌握事物的客观规律（模型） 。

要知道，这些经典模型固然经典，但是到了实际应用中，它们并非神圣不可稍加改变。也不是说机器学习就仅限于这些经典模型。

只有掌握了机器学习精髓的人，才可能灵活运用现有模型去解决实际问题，甚至进一步针对具体问题发明自己的模型和/或算法。

反复学习，从记忆到掌握

当然，达到这种程度并非一撮而就，总要从最简单的模型开始。

根据我的经验，即使是本课列出的这几个最常用也相对简单的模型，要真正掌握，都需要反复学习。

有可能第一遍看完有点似是而非，或者感觉自己明白了，但要自己从头推导又会半截断片儿。

就像刚学完又忘掉生字，或是背诵到一半想不起后续99乘法表的小学生，这都是非常正常的现象。真正原因，就是还没有真正掌握。

反复多学几遍，从头到尾掌握整件事情的逻辑，知道一个模型是怎么从最初设定目标，到一步步实现目标的——当真正掌握了这个过程之后，再回头看一个个具体的模型，每一步都是顺利成章的。

掌握了事物内在的逻辑性，再去记忆，就容易多了。

学习标准设置得不必太高，比如可以这样：

第一遍学，只要求自己能完全掌握机器学习数据、模型、算法相互作用的基本关系，训练过程和评价标准。具体的模型，掌握最简单的线性回归就可以。

只要 end2end 掌握了第一个模型，做到：能够从模型函数开始推导出目标函数，再用梯度下降算法求解，用（伪）代码实现梯度下降求解过程。

第一遍学习掌握一个模型；第二遍学习就不难掌握2-3个模型；第三遍就有可能掌握本课列出的大部分模型………如此 由易到难，螺旋式推进。

对于一些数学模型本身就比较复杂的，比如条件随机场、隐马尔科夫这类涉及场论和势函数的模型。

如果直接入手，往往会被卡在模型函数本身上。但是当有了前面几个模型的基础，了解了更抽象层面的原理，掌握起来就容易多了。

数学需要多精深？

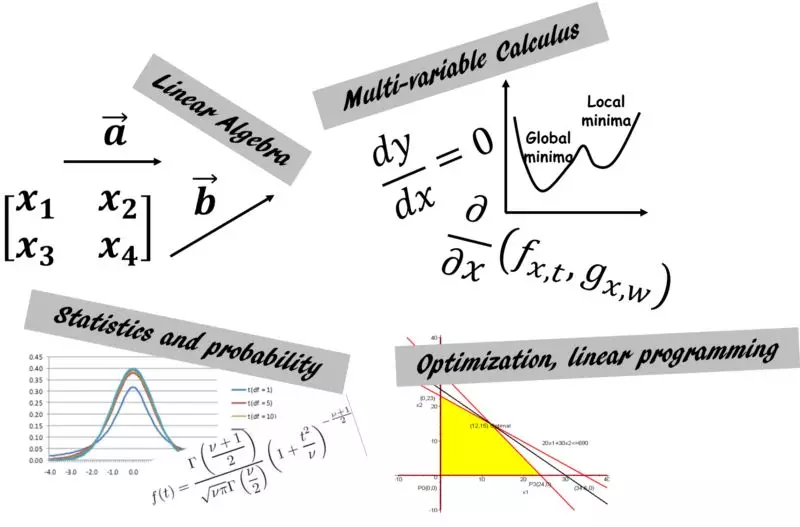
很多同学，想学机器学习。但是一上来就看模型，看到一大堆炫酷的公式，往往感觉很吓人。

有些人也就因此萌生退意，要么放弃，要么只用现成工具把模型当作黑盒使用。

其实，学习经典模型，并不需要多么精深的数学功底，理工科大学本科的数学课就基本够用了。

基础数学概念

在学习的最初阶段，只要：

  • 学过坐标系

  • 了解函数、向量和矩阵的概念

  • 能从直观角度对求导、求微与函数的关系有所理解

  • 并掌握最简单的矩阵运算

就可以对本课中的经典机器学习模型有一定深度的感性认识了。

本课中的公式都是减了再减的，务必要掌握。如果实在数学工具掌握太少，最次最次，也至少要读懂一组公式推导中的第一个和最后一个式子

  • 读懂它们都针对哪些变量进行了怎么样的运算

  • 这些变量和运算对应的物理意义是什么

  • 第一个式子是对哪种真实场景的数学描述

  • 最后推导的结果又具备怎样的特征

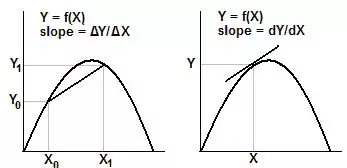
初次学习者，可以暂且掌握到这个深度。

两条路径反刍数学知识

当然，仅仅这样的程度，套用现成模型还将就，却不可能达到灵活运用的程度。

所以，还是建议同学们力求理解每一步推导过程。

如果有可能，可以事先复习一下大学本科的高数（数学分析）、概率统计和线性代数课本。

或者，在学习模型的过程中，一旦遇到了数学上的阻碍，就回头去查找相应知识。

制定数学知识速查手册

很多数学问题，之所以让人头大，其实并不是真的有多难，而是符号系统比较复杂，运算繁复，或者运算所表达的物理意义多样。

很多时候造成困扰是因为想不起来这里用到什么定理，哪个公式，或者这样操作表达的含义是什么了。

如果把常用的细小知识点都记录下来，按主题整理在一起，做成速查手册（小字典），需要用的时候迅速查找一下对应点，效果往往意想不到地好。能让我们学习“机器学习”的道路顺畅不少。

日常学习 Tips

关联

把新学到的东西和日常的工作、生活联系起来，进行思考。比如：将理论代入现实，不同领域间事物的类比，相似内容的对比等。

以身边的实例来检测理论。不仅能够加深理论知识的理解，而且有助于改进日常事物的处理方法。

记录

准备一个笔记本，纸的或者电子的。有什么发现、感想、疑问、经验等等，全都记下来。

如果是对某个话题、题目有比较完整的想法，最好能够及时整�