实时翻译的发动机矢量语义斯坦福大学课程解读
转载自公众号: 人工智能头条
大家好,我是为人造的智能操碎了心的智能禅师。
GraphDB 最近刚刚升级到 8.7 版本,此次特别更新了矢量语义包,直接以插件形式整合到程序中。
矢量语义在 NLP 领域,有着非常重要的意义,它用矢量的方式,加快了计算机学习新词汇的速度。让机器翻译、实时翻译、聊天机器人智能化等,成为可能。
预备知识
回想一下我们读书时候,碰到不认识的词是如何操作的。
一种方式是直接查字典;另一种方式是先不理会这个词,继续往下阅读,当你越来越多的读到包含这个词的句子,词的含义也开始逐渐清晰起来。

来源:Reaching Higher NH
传统 NLP,比如之前禅师发过的文章,类似查字典的方式,很可能导致词义和上下文脱节。例如 one-hot encoding,他认为“狗”和“猫”就是两个东西,即使你在下文中,明确指出来他们都是动物、都是宠物。
很明显,这种方式去做分词、打标签还可以,要想实现翻译、甚至聊天功能,那简直是不可能。
举个例子。 Tesgüino 这个词,估计没几个人认识,机器自然也不只是。但是当我们有了下面 4 个句子:
-
桌子上有一瓶 Tesgüino
-
大家都喜欢 Tesgüino
-
Tesgüino 能喝醉
-
Tesgüino 是用玉米制成的
很容易就能联想出,Tesgüino 是一种酒(能喝醉);是装在瓶子里,用玉米制成。
虽然还是不知道 Tesgüino 什么样子,闻起来什么味道,喝起来什么感觉,但我们已经能够想象出这东西可能和高粱酒、伏特加、龙舌兰差不多,可能还更好喝一点(大家都喜欢)。
就这样,通过一个新词周边的近似词,我们也能推测出这个新词的含义。
单词向量是一行实数值(与虚数相对),其中每个点捕获单词的含义的维度,并且语义上相似的单词具有相似的向量。
所以我们只要计算出语义向量的相似度,就能很好的解决 NLU。那么接下来,考验智商的时刻到了(如果实在看不懂,拉到文末,相信会对你有所帮助)!
有请 NLP 一线开发者罗周杨,为大家解读一下斯坦福经典 NLP 课程中,矢量语义向量相似度计算。
关于罗周杨:
某互联网公司 NLP 开发者
最不喜欢的语言:JavaScript
推荐的电脑软件:Jetbrains 全家桶
推荐3本书:《Java编程思想》《深入理解计算机系统》《深度学习》
向量
文档和向量
如果用向量来表示一个文档,该怎么表示呢?
我们再莎士比亚的4部作品里(文档),找了4个词,我们统计各个单词在文档中出现的次数,可以得到一张表格:

上面表中,有4个单词,所以每一个文档可以表示成一个由单词频率组成的向量:

如果单词有很多个,假设是N,那么每个文档就可以表示成一个N维的向量。可见,这样的向量表示是稀疏的(sparse)。
单词和向量
除了文档可以表示成一个向量,单词也可以。
和文档类似,我们可以统计出一张表格,但是不同的是,我们不是统计单词的个数,而是统计两个单词出现在一起的频数。看一张表格你就知道了:
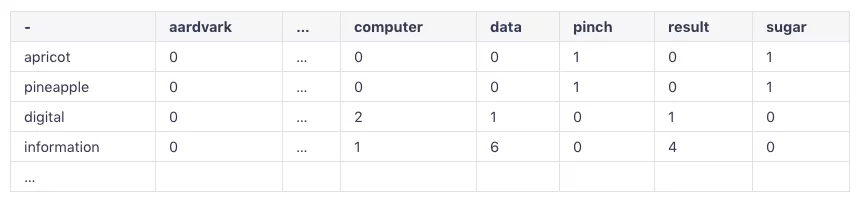
这个表格是一个 V×V 的表格,每个数字表示当前列的单词出现在当前行单词后面的次数,这就构成了上下文,所以这个表格其实就是一个上下文矩阵,其中 V 就是总的词典的大小,也就是单词的数量。
我们取出每一行,就可以得到一个单词的向量表示,例如:
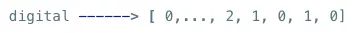
同样的,这样的表示也是稀疏的。
Cos 计算相似度
现在我们已经有文档或者单词的向量表示了,那么该如何计算它们之间的相似度呢?一个很常见的方法就是余弦相似度(Cosine similarity)。
学过高中数学就知道,两个向量的点积(dot-product)或者内积(inner product)可以由以下公式计算:
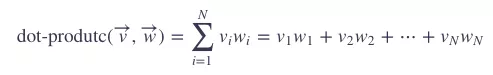
而向量的模(vector length)为:
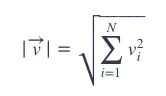
又:
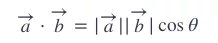
即:
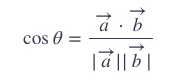
所以,我们可以计算
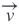 和
和
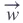 的余弦值:
的余弦值:
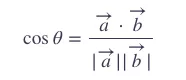
所以,两个向量的余弦值越大,它们越相似。接下来就要介绍TF-IDF了。
TF-IDF
首先解释一下这个词:TF-IDF = Term Frequency - Inverse Document Frequency
其中 term-frequency 是单词
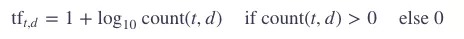
在文档中出现的次数,
那么什么是 IDF 呢?首先我们弄清楚 DF(document frequency)。
DFT 表示出现过这个单词的文档(document)的个数。
那么,IDF就是:
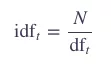
其中,N就是一个集合(collection)中的documents数量。
为了避免数值过大,通常会取对数:
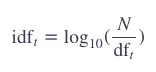
至此,我们可以计算这个单词 t 的 tf-idf 权值:
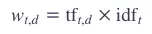
此时,我们的第一个表格,就变成了:

到目前为止,上面的所有向量表示都是稀疏的,接下来要介绍一种稠密的(dense))的向量表示: word2vec。
Word2Vec
这个大家应该很熟悉了,应该算是NLP领域的标配了。,但是如果你没有一点基础的话,有些概念还是难以理解。想要相对完整地理解 word2vec,你需要结合多方面的资料。
TensorFlow 有一个教程《Vector Representations of Words》,文末扩展阅读也给出了参考链接。
Word embedding
首先我们解释一下词嵌入(word embedding)的概念。咱们之前的所有向量表示都是稀疏的,通常都是一个高维的向量,向量里面的元素大部分都是0。那么 embedding 有什么不一样的呢?
Embedding 同样也是用一个向量来表示一个词,但是它是使用一个较低维度、稠密地表示。
如果使用之前的稀疏表示,你可能会这样表示 hello 这个词语:
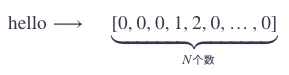
使用 embedding 表示后:

其中的差异一眼就看出来了。所以很明显,word embedding有好处:
-
不会造成维度爆炸,因为维度是我们自己设置的,通常比较小
-
向量是稠密的,不需要稀疏向量所采用的各种优化算法来提升计算效率
词嵌入理解了,那么什么是word2vec呢?其实就是把单词表示成固定维度的稠密的向量!说起来简单,但是也有很多小技巧的。
数据模型
假设我们有一个很大的文本语料,我们需要用这个语料来训练出单词的向量表示。那么该怎么训练呢?
word2vec 有两种常用的数据准备方式:
CBOW,用前后词(context words)预测目标词(target word) skip-gram,用目标词(target word)预测前后词(context word)。
我们用一个英语标准的测试键盘按键是否工作完好的句子开始:
the quick brown fox jumped over the lazy dog
这句话里包含了所有的英文字母。假设我们的窗口大小(window size)是2,目标词选择 fox。
如果是 skip-gram 模型,我们会这样准备数据:

也就是一个目标词,我们可以构造出 window_size 个训练数据对。
如果是 CBOW 模型,我们会这样准备数据:

看出其中的差异了吧?
总之,skip-gram 和 CBOW 就是两个相反的数据模型。Learning Word Embedding有两张图可以分别表示两种模型的输入方式:
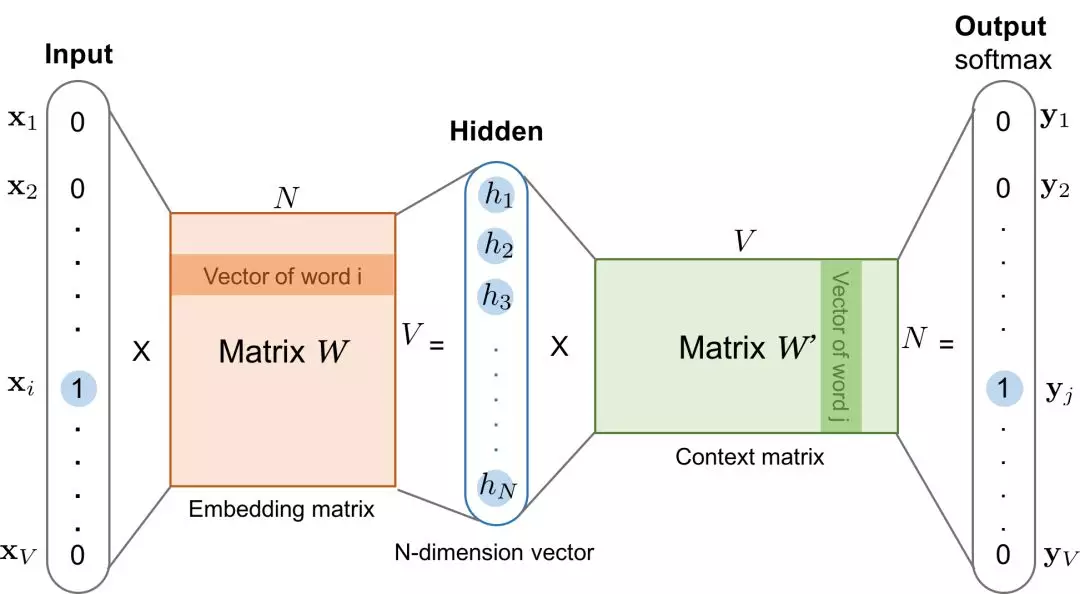
👆skip-gram 模型
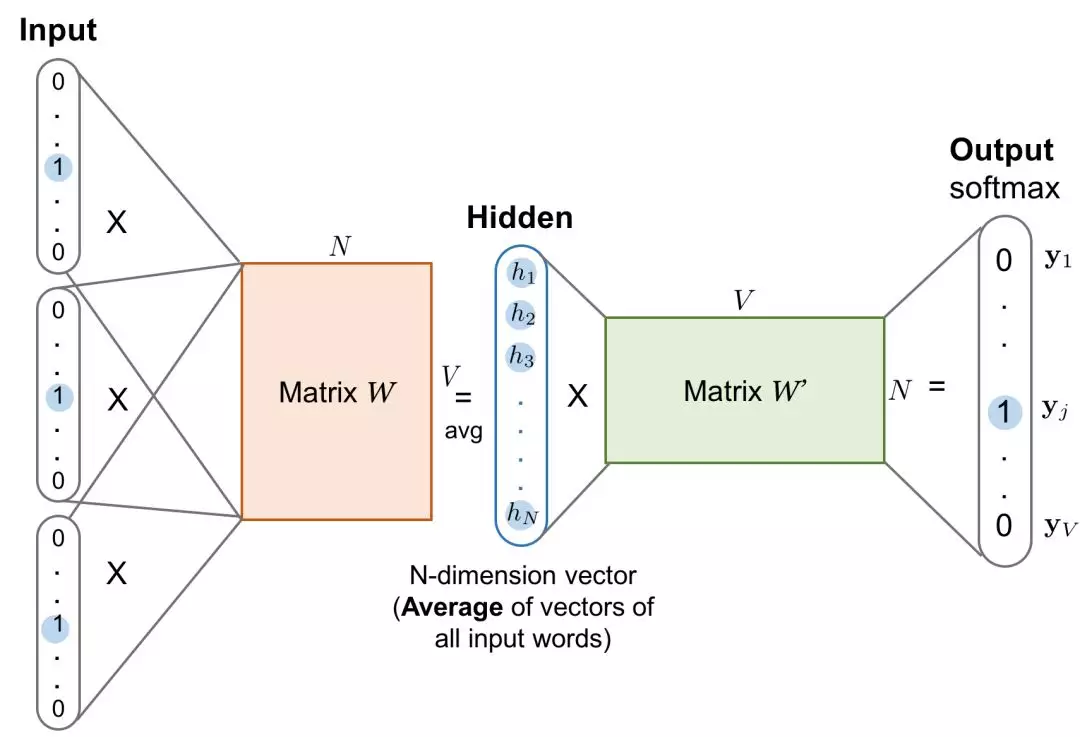
👆CBOW 模型
数据模型应该清楚了。
与之前不同的是,word2vec 并不关心相邻单词之前一起出现的频数,而是仅仅关心,这个单词是不是属于另一个单词的上下文(context)!也就是说,word2vec 不关系根据这个词预测出的下一个词语是什么,而是只关心这两个词语之间是不是有上下文关系。
于是,word2vec 需要的仅仅是一个二分类器:“这个单词是另一个单词的上下文单词吗?”
所以,要训练一个 word2vec 模型,我们其实是在训练一个二分类器。而二分类器,你肯定很容易就想到了 Logistic Regression。
实际情况,skip-gram 用的比较多,因为有一个说法,CBOW 模型在小的数据集上面表现不错,在大的数据集里,skip-gram 表现更好。
神经语言模型
这里需要说明进一步说明一下。 TensorFlow 里面有关于神经概率语言模型 (nerual probability language model) 的描述。
传统的神经概率语言模型的训练通常是用最大似然 (maximum likelihood) 法则来最大化下一个词的softmax概率,基于前面的词,也就是:
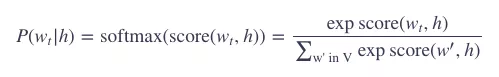
其中,score(wt,h) 其实就是 wt 和 h 的点积 (dot-production)。
那么这样训练模型的目标就是,最大化对数似然概率 (log likelihood):
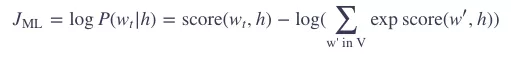
这样的问题是 计算量太大了,因为在每一个训练步里,需要对词典里的每一个词,使用 softmax 计算出一个概率值。这个模型如下图所示:
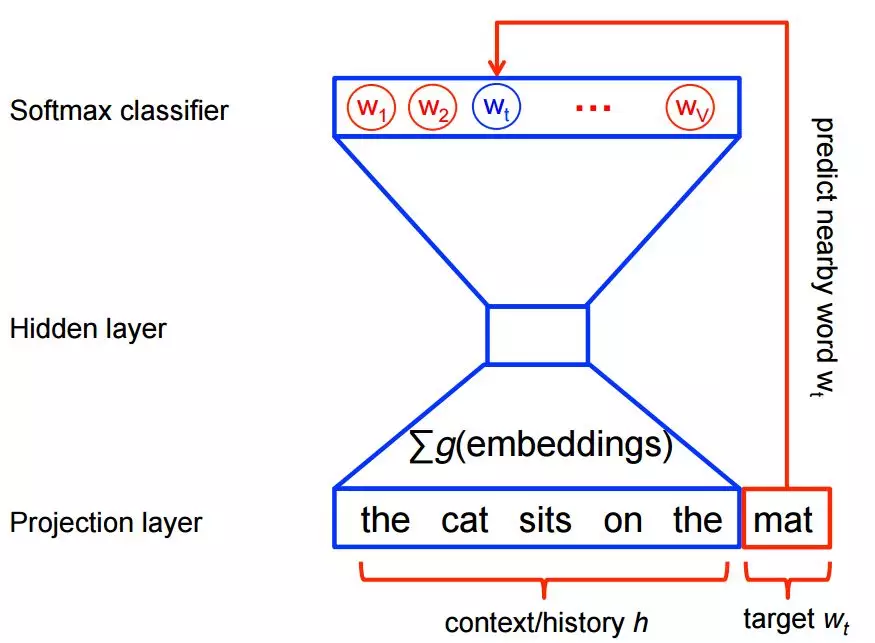
正如前面所说,我们的 word2vec 并不需要一个完整的概率模型,我们只需要训练一个二分类器,从 k 个噪声单词 (noise words) 里面判别出正确的目标词 (target words)。
这 k 个噪声单词是随机选择出来的,这个技术叫做负采样 (negative sampling),因为选出来的一批词都是不是正确的 target word。这个模型如下图所示:
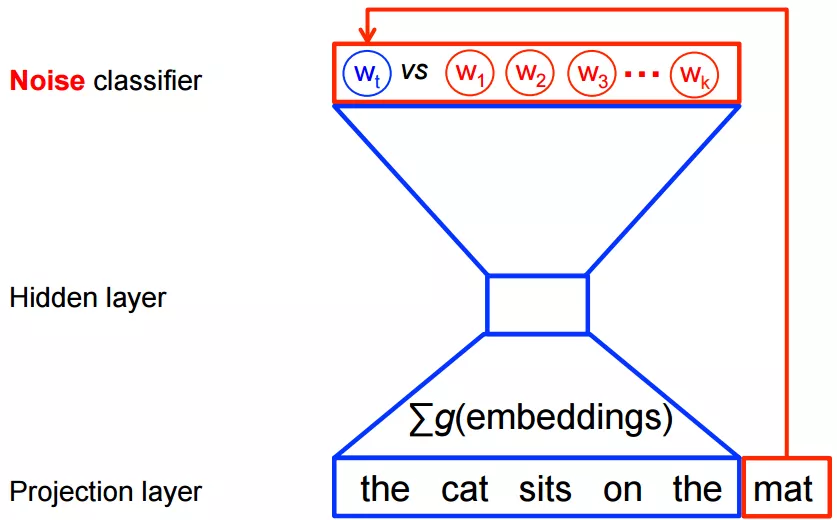
这样一来,我们要最大化的目标就是:
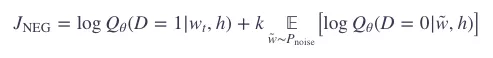
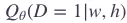 表示二分类逻辑回归在数据集 D 中的上下文 h 中包含目标 wt 的概率。
表示二分类逻辑回归在数据集 D 中的上下文 h 中包含目标 wt 的概率。
The classifier
上面说到了负采样。什么事负采样呢?其实就是随机选取k个词语,和目标词组成负样本训练。
现在我们回到斯坦福的教材上来。这里列出训练一个 skip-gram 模型的要点:
把目标词和上下文词组成的样本当做训练的正样本 (positive sample)
随机选取一些词和目标词组成的样本当做训练的负样本 (negtive sample)
使用 logistic regression 训练一个二分类器来区分两种情况 regression 的权重就是我们的 embedding word2vec 需要的是训练一个 binary logistic regression,给定一个目标t和候选上下文 c 的元组 (t,c),返回 c 正好是 t 的上下文词的概率:
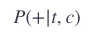
那么,c 不是 t 的上下文词的概率就是:
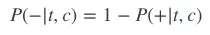
那么分类器如何计算这个概率 P 呢?skip-gram 模型有这样一个假设:相近的词它们的嵌入表示也很近。
也就是,我们可以把两个词语的嵌入表示的相似度,用来表示概率 P。相似度就用我们上文说到的余弦相似度:
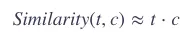
当然,点积的结果并不是概率表示,我们需要用 logistic 或者叫 sigmoid 函数,把它转化为概率表示:
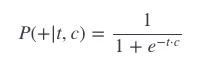
那么:
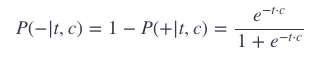
上面的公式只是一个单词的概率,但是我们需要把整个 window 里面的单词计算进来。skip-gram 模型还有一个假设:所有的上下文单词之间是独立的。
假设我们的 window_size = k,于是有:
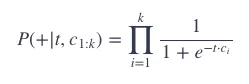
通常,我们会使用对数概率:
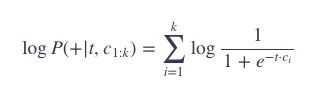
skip-gram 模型的训练
为了训练这个 word2vec,我们除了正样本,还需要负样本。实际上,负样本通常比正样本更多。一般用一个比率k来控制正负样本,如果 k=2 则说明,每一个正样本,对应2个负样本。这就是前面说的负采样技术。
构造负样本选择的词语(噪声词 noise words)是根据一个频率来的:
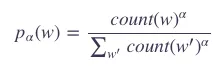
其中,α是一个比率,一般来说取值
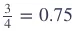
为什么需要这个比例呢?这样可以让出现次数少的词被选择的可能性变大。
举个例子,如果没有这个比率,假设P(a)=0.99,P(b)=0.01,加上这个比率之后:
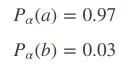
可见,b得选择的概率从0.01提升到了0.03。
有了正负样本之后,我们的模型训练就有以下目标了:
-
最大化正样本的概率,也就是正样本的相似度最大化
-
最小化负样本的概率,也就是负样本的相似度最小化
在整个训练集上,用数学表示出上面的目标就是:
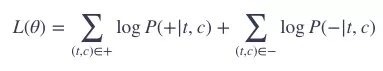
如果从单个训练数据对来看(一个 (t,c) 对和 k 个噪声 n1,n2,…,nk),就有:
概率P由simoid函数计算,有:
展开,有:
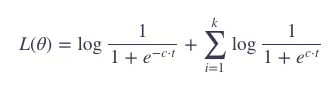
可以看出,最大化上面的目标,就是最大化正样本 c⋅t,同时最小化负样本 ni⋅t。
有了上面的概率表示,那么我们就可以使用交叉熵作为损失函数,然后训练模型了。
值得注意的是,TensorFlow 里面把上面的两个过程合并了,合并在 tf.nn.nce_loss 这个函数里面。你可以看到 TensorFlow 的教程里面的损失函数就是使用的 tf.nn.nce_loss 作为损失函数。但是你继续追踪源码就会发现,这个损失函数只不过是:
-
进行采样,计算出概率
-
使用交叉熵计算损失
可见,和我们上面的训练分析过程是吻合的.
两个权重矩阵W和C
还记得我们上面 skip-gram 模型训练的最后一个要点 regression 的权重作为 embedding 吗?
其实,word2vec 训练之后会有两个权重矩阵,分别是嵌入矩阵 W 和上下文矩阵 C,回顾一下这张图:
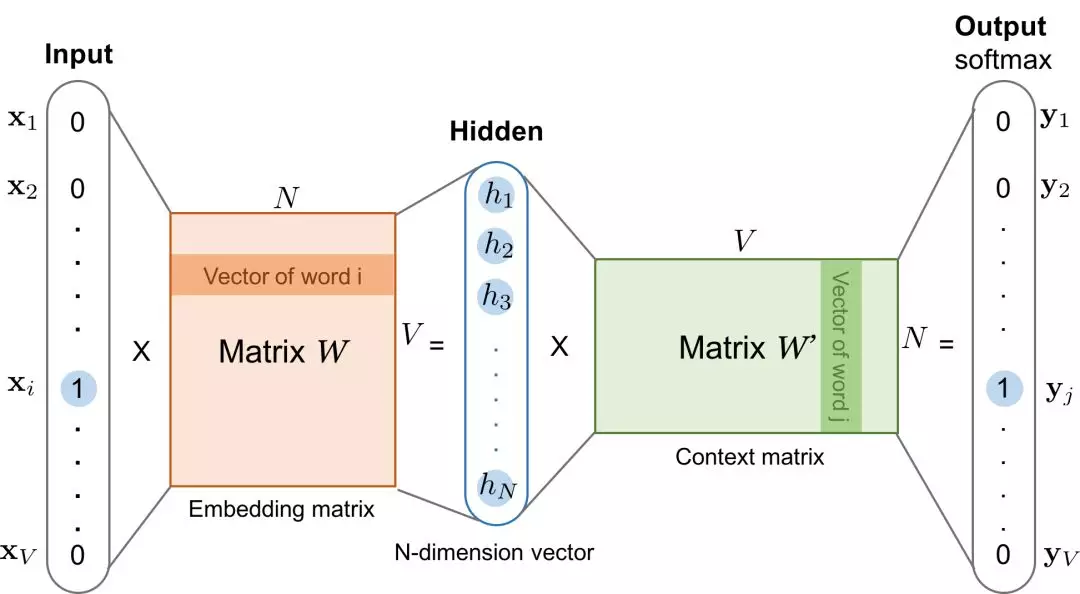
上图中的W权重矩阵就是我们的 embedding 矩阵,而 W′ 权重矩阵就是我们的 Context 矩阵.
如果我们要得到每一个单词的向量表示,只要从 W 中取出对应的行即可!因为,训练的每一个单词,都是用 one-hot 编码的,直接和 W 相乘即可得到改词的向量表示.
所以,整个 word2vec 模型就是一个浅层的神经网络.
我们训练结束后,得到�
- 原文作者:知识铺
- 原文链接:https://index.zshipu.com/geek/post/%E4%BA%92%E8%81%94%E7%BD%91/%E5%AE%9E%E6%97%B6%E7%BF%BB%E8%AF%91%E7%9A%84%E5%8F%91%E5%8A%A8%E6%9C%BA%E7%9F%A2%E9%87%8F%E8%AF%AD%E4%B9%89%E6%96%AF%E5%9D%A6%E7%A6%8F%E5%A4%A7%E5%AD%A6%E8%AF%BE%E7%A8%8B%E8%A7%A3%E8%AF%BB/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


