分享嘉宾：观宙 阿里飞猪 算法专家

编辑整理：王吉东

出品平台：DataFunTalk

导读： 在飞猪搜索CPC广告业务中，广告策略不仅需要考虑CPC消耗和广告主ROI，平台整体营收 ( 即CPC消耗+自然交易抽佣 ) 也是不能忽略的优化目标。传统上基于广告pCTR、pCVR、bid等因子的策略算法仅仅从广告曝光本身来对广告主、平台和用户的利益进行优化，难以准确调优这一平台整体目标。

我们通过引入因果推断技术，将广告投放建模为对搜索产品的干预 ( intervention )，直接预测广告投放与否对业务目标产生的uplift效应，作为下游优化问题的线性奖励 ( rewards ) 或约束 ( constraints )，以支持各类线上策略。

在本文，我们从其中预算分配策略的视角，介绍飞猪广告算法如何利用广告效应模型进行业务目标优化，同时也介绍模型底层特征 ( 如CTR、CVR ) 的一些建模经验。主要内容包括：

  • 平台视角下的广告预算分配
  • 因果推断技术
  • 因果推断在广告策略中的实践
  • 未来思考

01 平台视角下的广告预算分配

1. 预算分配：多目标优化问题

广告策略（或者说预算分配），本质上是一个多目标优化的问题。下面结合一个示例简述一下这类优化问题的目标和约束。

从平台角度上来讲，预算分配的优化目标往往是包含多种复杂的因素的函数：

  • 平台变现效率（即ecpm）
  • 广告点击率（ctr_{ad}）
  • 广告转化率（cvr_{ad}）
  • 广告主收入（gmv_{ad}）
  • 平台利润（revenue_{ad}）

同理，从约束角度看，主要包含以下约束：

  • 广告主总预算（budget）
  • 投放计划的投资回收率（ROI）
  • 点击率下限（ctr_{thres}）
  • 广告主收入下限（gmv_{thres}）
  • 平台利润下限（revenue_{thres}）

另一方面，对于平台中的不同的业务，不同的用户，甚至不同产品不同的投放单元，具体的目标和约束也会存在较大差异。针对不同的目标和约束，需要使用不同的因子加以控制。

2. 常用控制方法和控制对象

常用的控制算法包括：

  • PID：最常用的一种传统的工程方法
  • 对偶法：基于线性规划求解拉格朗日系数，得到影子成本，通过影子成本进行线上控制
  • 线性插值法：通过历史数据拟合控制变量与目标变量的关系

以上提到的几种方法有一个共同的特点：都基于线性模型，因此，要想达到有效的控制，就需要线性因子。

常用的控制对象包括：

  • 广告主的出价（bidding）
  • CTR/CVR准入下限
  • 参竞概率

3. 使用因果推断的语言建模

广告策略问题，常用的策略因子包括：

  • CTR预估（pCTR）
  • CVR预估（pCVR）
  • 出价胜出概率分布（Bidding Landscape）

然而，以上的策略因子具备局限性。以GMV为例，对平台GMV进行控制，仅使用pCTR、pCVR等策略因子是不够的。因为从业务角度看，在电商领域，原生广告和产品（包括搜索、信息流等）的相似度很高，因此广告投放的分布和对应原生产品的分布是相似的；这样带来的结果就是，当广告的CTR/CVR高的时候，自然产品的CTR/CVR往往也会很高；我们不能基于较高的CTR/CVR预估结果推测广告投放的真实效果。

基于此，引入本文的主题——使用因果推断建模。

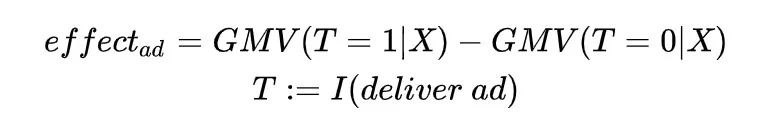
  • 公式中的参数T可定义成是否投放广告的indicator变量
  • 模型控制目标是平台的收入（即GMV）
  • 建模问题定义为广告投放对平台KPI的影响，即在给定特征的前提下，投放广告的GMV减去不投放广告的GMV得到的收益

只有通过建立上述模型，才能优化广告投放的真实效果，实现平台和广告主的共赢。该模型涉及到的因果推断技术，将在下一章节详细阐述。

02 因果推断技术

1. 基本问题

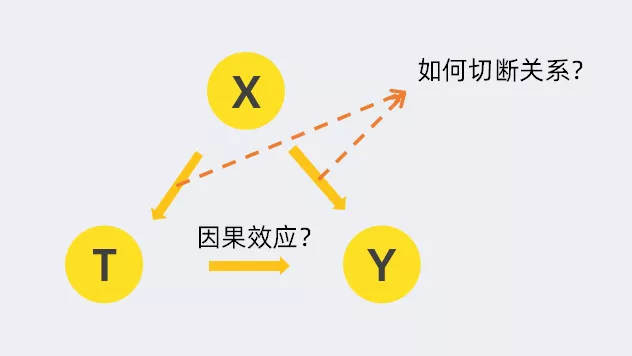
将前文所述的模型抽象成上图所示：我们需要建模的是T对Y的影响（T即是否投放广告这个动作；Y是平台的某项KPI，如GMV）。

然而影响平台建模的因素很多，比如不同活跃度的用户、不同的时间段、不同的行业等，都会影响广告在搜索推荐中的转化效率。

2. 影响因素的控制和约束

如何在这种复杂的数据关系中提取出广告投放对平台的GMV产生的影响？一个较为朴素的方法就是控制变量法，即人为控制和约束除了广告投放之外的其他相关因子。

具体来说，有两类实现路径：

① 随机实验（切断X->T）：假设T是随机分配的，即T与任何变量独立；

② 特征工程（切断X->T，X->Y）：假设X包含所有的confounders。

  • 定义confounders：同时影响T和Y的变量
  • 若给定X，则不同treatment group下影响Y的协变量分布相同，即X->Y是天然的随机分配

基于以上这两条假设，从数学上理解，其核心是比较投放广告与否的前提下，平台KPI的期望：

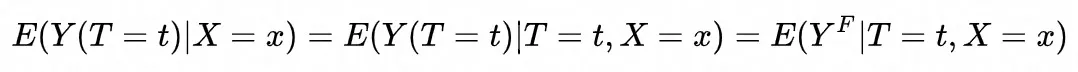
由于X与Y/T独立，故添加条件概率不影响最终的期望值；这样，待求解的期望值等同于实际样本分布的期望。从因果推断角度看，这是个比较理想的情况：从观察数据上得到的模型，和我们期望的因果效应相等的时候，就可以直接使用机器学习模型解决问题。

抛开数学公式，从常识角度也能解释以上假设：每组特征下可视为随机实验，得到局部的无偏估计；那么任意样本上的效应，可以在相应的X的分布上积分得到。

3. 从机器学习视角审视

前文简述了一些因果推断领域的技术背景，下面从机器学习视角审视这个问题，将会遇到两个挑战：

**样本结构方面，对两组样本（T=0和T=1）的分布要求更加严格：**

  • 对于一般的预测问题，只需要保证样本整体无偏，即可预估
  • 对于因果推断问题，除了样本整体无偏，还需要要求两组样本的结构相近；否则会存在误差累计效应

对变量T的推断准确度要求更高，这并不是机器学习所擅长的工作：

  • 传统的统计模型，通过对数据引入假设，可推断参数分布
  • 大数据时代的算法模型，往往关注预测精度而非统计推断能力

4. 样本结构问题

基于前文提到的两个挑战，首先讲述样本结构问题的处理办法。

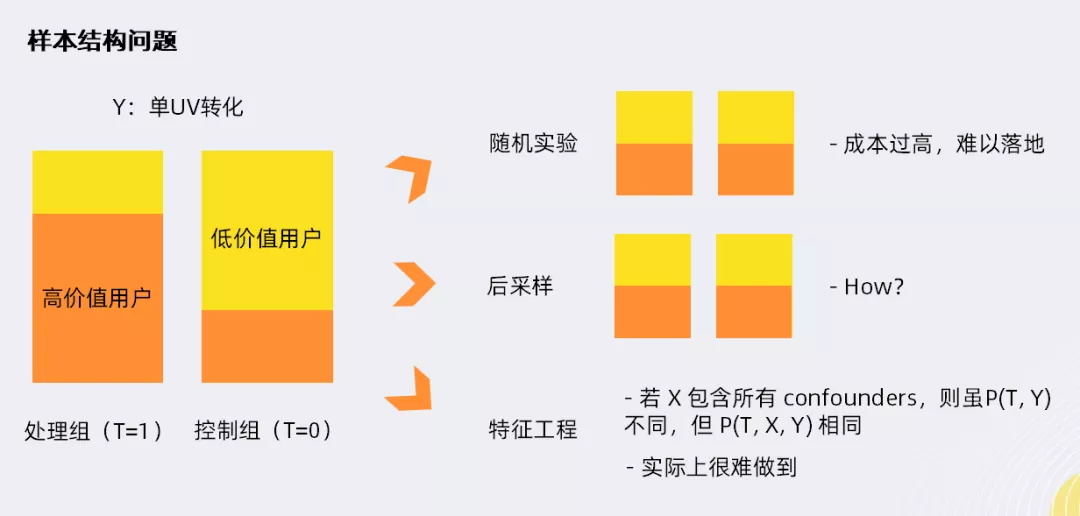
从业务角度列举一个简单示例：控制目标Y是归一化（即单UV转化）后的平台GMV；处理组和控制组的用户分布有明显差别（处理组的用户价值较高，控制组的用户价值较低）。

有3种方法可以解决这类问题：

① 随机实验

  • 选取部分流量，线上广告随机投放，不采用任何策略
  • 成本过高，难以落地

② 后采样

  • 通过重采样方法，使两组样本分布一致

③ 特征工程

  • 机器学习常用方法
  • 假设X包含所有的confounders，则虽然两组样本的P(T,Y)不相同，但P(T,X,Y)相同
  • 实际很难做到，且对样本也有较高要求

在后面的章节中会详细介绍以上方法在广告策略实践中的具体应用。

5. 变量的统计推断问题

第二个问题是变量的统计推断问题：在大数据时代常用的复杂模型中，如何精准推断某一个变量的效应？具体到我们的广告策略场景上，就是如何推断广告是否投放这个干预变量对平台的KPI产生的影响。

这类问题其实是很多学科里面临的一个终极问题，很难得到真正解决。具体到工程实践上，我们可以通过一个模型结构先验和loss设计，促使模型对这一单变量学习到正确的效应。

03 因果推断在广告策略中的实践

1. 特征工程

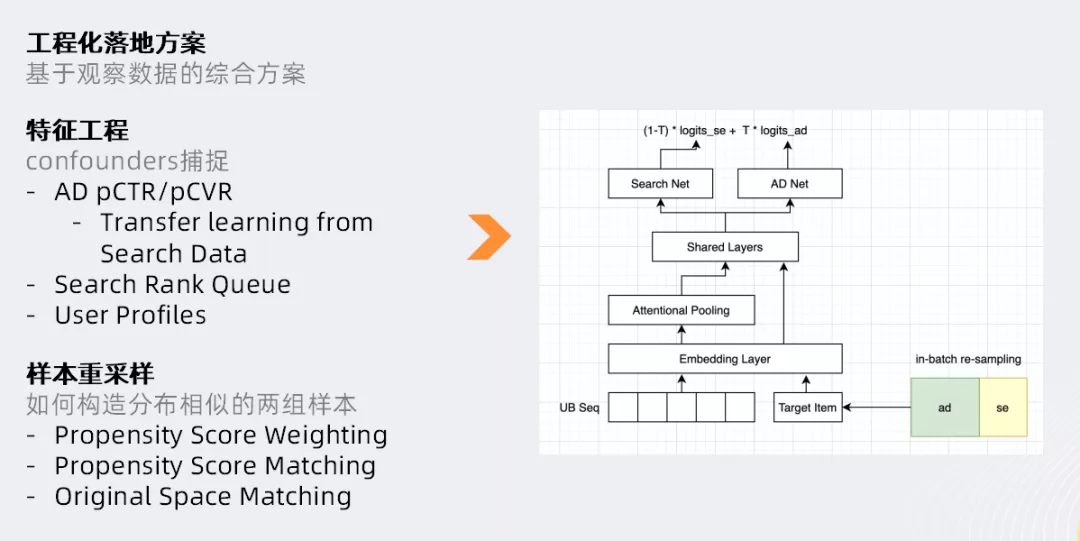
先从前文提到的两大分支（特征工程，样本重采样）入手，具体讲述工程落地的方法。

特征工程方面，目标是捕捉到所有的confounders（即影响到广告是否投放，以及影响到我们的平台效率的所有特征）。

首先参考广告系统里其他常见工作，例如广告的CTR/CVR预估模型；该类模型对广告效率的预估，会预先将原始的复杂特征做汇总。基于此，整体的思想就是基于原生的广告搜索模型做迁移学习。

然而，搜索推荐的信息流和广告策略的数据，两者的分布往往存在差异；因此会涉及到模型的泛化性能问题，需要对模型的拟合精度和泛化能力做权衡。具体来讲，通过策略采样的方式（模型结构类似CTR/CVR多任务模型，但是样本和模型训练方式完全不同于CTR/CVR），将原生信息流样本和广告样本作为两个任务分别学习，最后通过loss融合实现多任务学习。

对于刚刚提到的模型精度和泛化能力的权衡的问题，我们采用in-batchre-sampling的方式，对于每个训练batch，通过超参去动态调整原生样本和广告样本的占比。

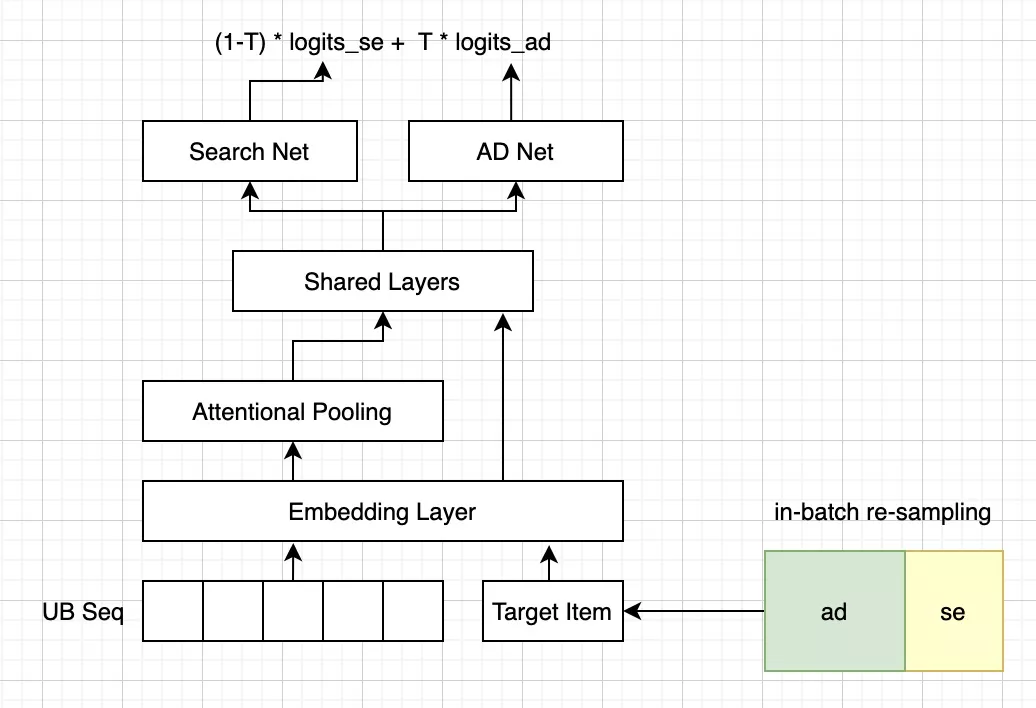
除了刚刚详细介绍的CTR/CVR，特征工程还包括广告系统中常用的Search Rank Queue（原生产品队列）、用户画像等，在此不做赘述。

2. 样本重采样

除了特征工程，另外一部分就是样本的重采样。对于纯观察数据，如何在避免AB实验的前提下，通过重采样方法在投放广告和不投放广告这两组的样本中构造相似的分布。

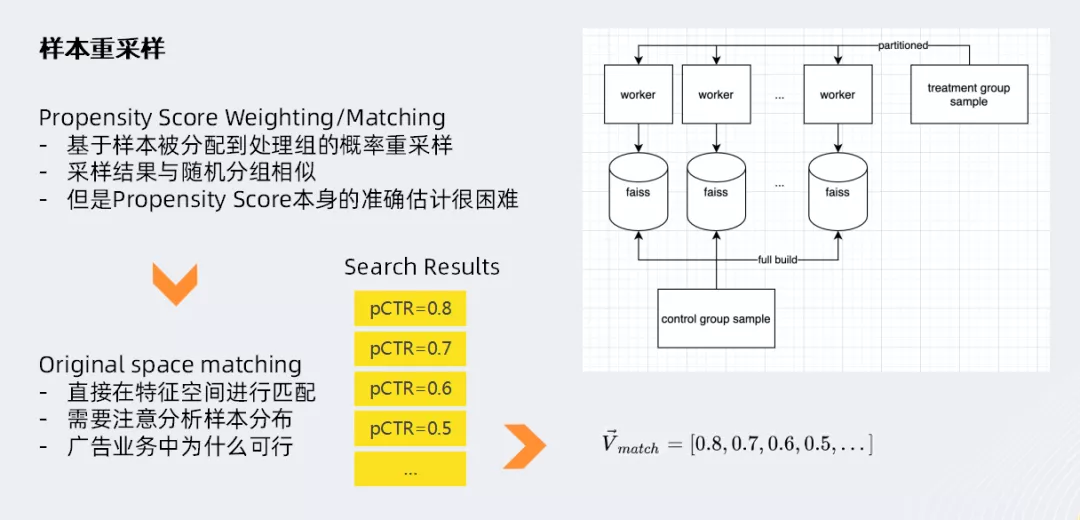
样本重采样常用的方法包括：

① Propensity Score Weighting/Matching（倾向评分加权/配比法）：

  • 基于样本被分配到处理组的概率进行重采样
  • 采样结果与随机分组相似
  • Propensity Score本身的准确度难以估计，不仅是用户行为用户偏好的高维分布，还受到广告本身的很多策略甚至一些产品业务规则的影响，较难进行机器学习建模，因此实际应用很难

② Original Space Matching（原始空间匹配法）等：

  • 避免预估Propensity Score，直接在特征空间进行匹配
  • 需要注意分析样本分布
  • 实际应用可行

以上述搜索结果页为例，每个商品都可以得到一个模型预估值（pCTR）。可以将整个页面pCTR的分布作为特征，用特征向量Vmatch表示；

首先对控制组（即未投放广告）的样本进行全量的索引构建；接着对处理组（即有投放广告），按照控制组的向量索引，使用KNN方法查找最相似的K个没有广告投放样本，进行配对。将控制组样本和处理组样本进行两两配对以后，很容易通过对比两组对应样本的转化率或GMV来描述广告投放与否对平台KPI产生的影响。

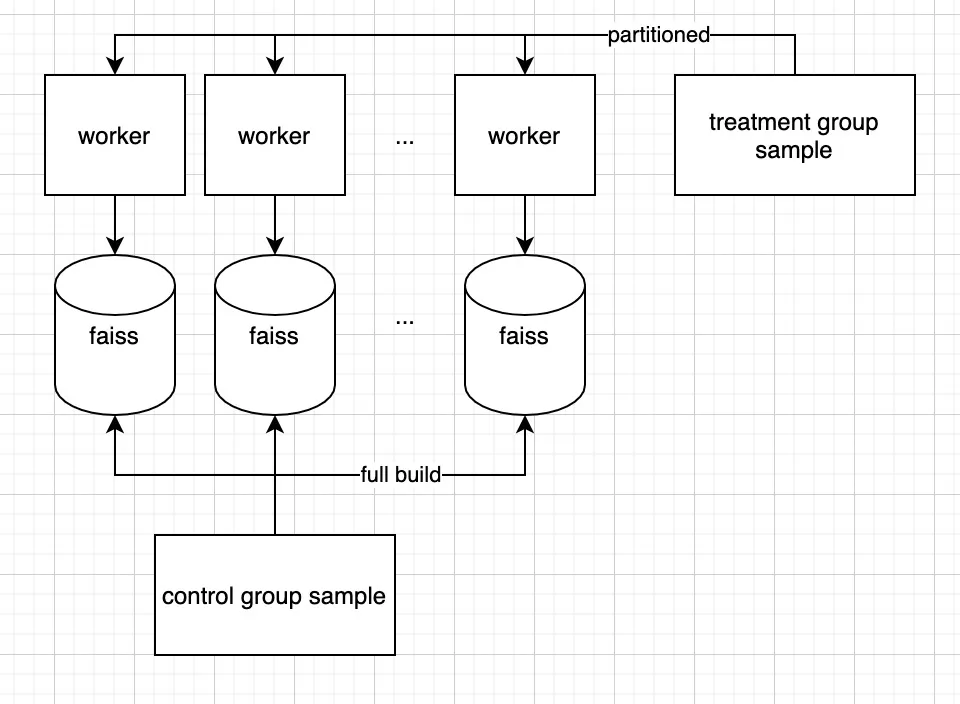
3. 模型设计

从模型设计角度，如何捕捉单变量的影响效应？前面提到过，这个问题很难得到真正的解决；但是我们有几个启发式的方法可以得到落地应用：

  • 借鉴ResNet思想，通过单变量embedding，结合深度网络短接（shortcut connection）将其接入到网络的最后一层，从而避免复杂的非线性因素的干扰
  • 借助迁移学习中的领域自适应技术（Domain Adaption），通过多任务学习来实现。具体来说，是将两组样本的投放广告与否，当作Multi-task的方式处理
  • 引入正则项（包括Structure Regularization、Task Regularization等），借助对业务的先验知识，对任务的loss加入正则项，促使模型学习到广告投放的效果

4. Uplift Evaluation简介

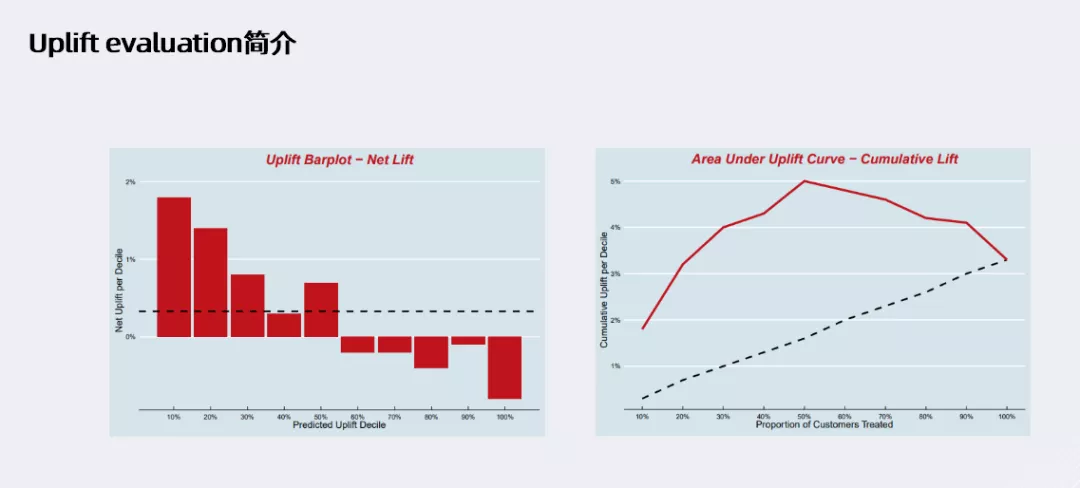
因果效应模型的评估，和常见其他用户模型的评估相比，最大的难点在于，每个样本都没有相反label。对于这类问题，业界常用分位数分析法进行评估，即对于每一类样本，按照广告效应的预测值，从大到小来进行分桶（上图左侧，分了十个桶）；每个桶内聚集广告效应的预测值相近的样本（包含不同的label）；将每组样本内的label的平均值相减，得到该组样本的uplift。

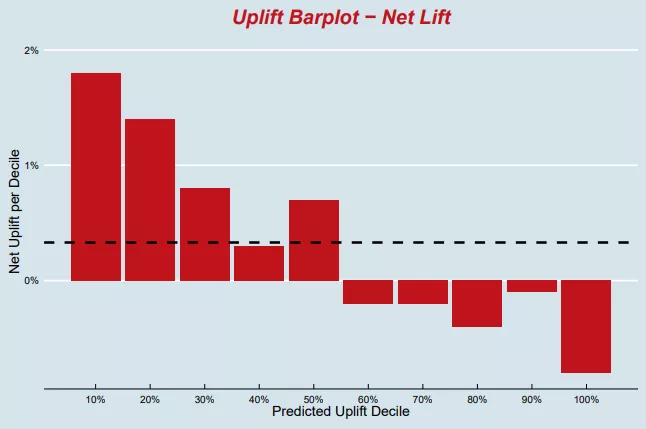
上图是个理想的情况：左侧贡献比较大，右侧贡献比较小，甚至是负的。基于柱状图做累计分布计算，得到下图：

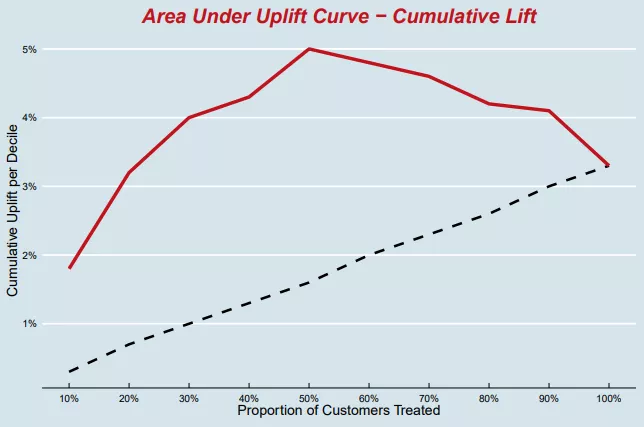
这个图和常规预估模型中的ROC曲线形似；同样，曲线下的面积（AUC）越大，模型预估效果越好。

5. 模型baseline：

Direct Method

假如我们直接做预估模型，选取SRP（结果搜索页，一部分是广告，一部分是非广告）的特征，和广告本身的特征（包括pCTR、pCVR，以及单个treatment的embedding）；模型预测某一条用户请求是否产生订单（listing to order）的概率。

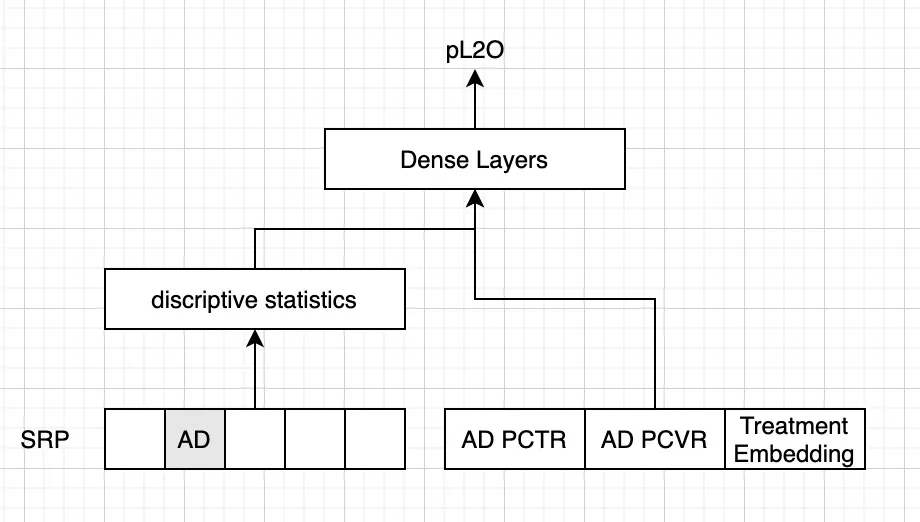
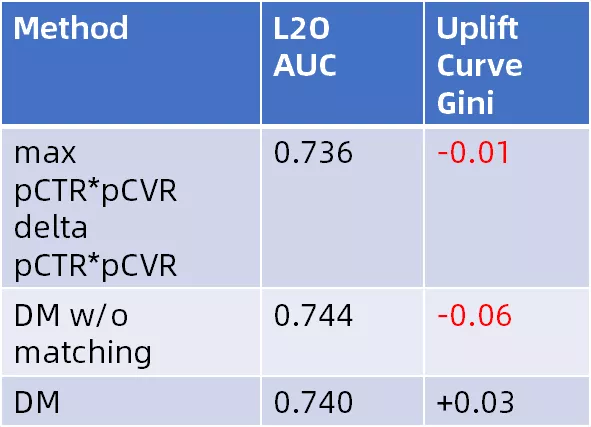
这类常用的预估模型，是将“广告是否投放”这一treatment作为一般特征。模型的baseline是基于pCTR/pCVR（包括最好商品的CTR/CVR，以及广告商品的CTR/CVR和最好商品的CTR/CVR的差距）进行预估，预估任务的AUC还算理想（0.736），但是评价广告效应的Uplift Qini指数是负值；增加DNN后AUC有所提升，但是Uplift指数会变得更差。

由此可见，预估任务的预测能力和对广告效应的评价能力并非正相关。

模型加入样本匹配后（表格最后一行），将样本调整成近似随机实验的样本，可以看出广告效应的预测能力就变成正向了。以上实验说明了针对Uplift进行建模优化的必要性。

6. 模型改进思路一：

Direct Method with shortcuts

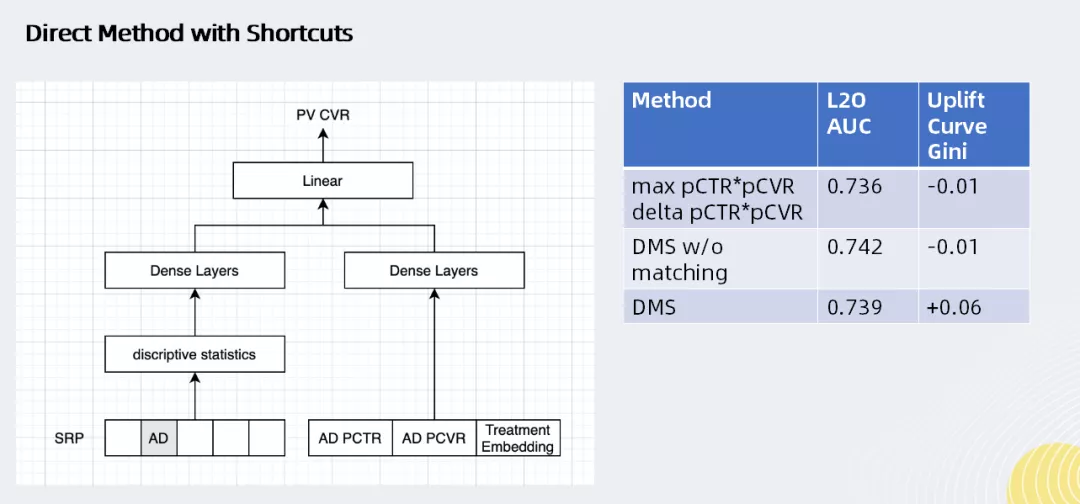
将所有特征都连到一个DNN里面，采用了ResNets的思想，如上图所示：左侧网络对用户搜索请求预期的转换效率进行建模，右侧网络对“广告是否投放”产生的影响进行建模，最后通过线性模型加以合并。对于广告效应的推断方面，这种模型相比于DNN会有一定的提升（uplift Qini指数提升至0.6）。

7. 模型改进思路二：

Dimain-Adaption: Multi-task Learning

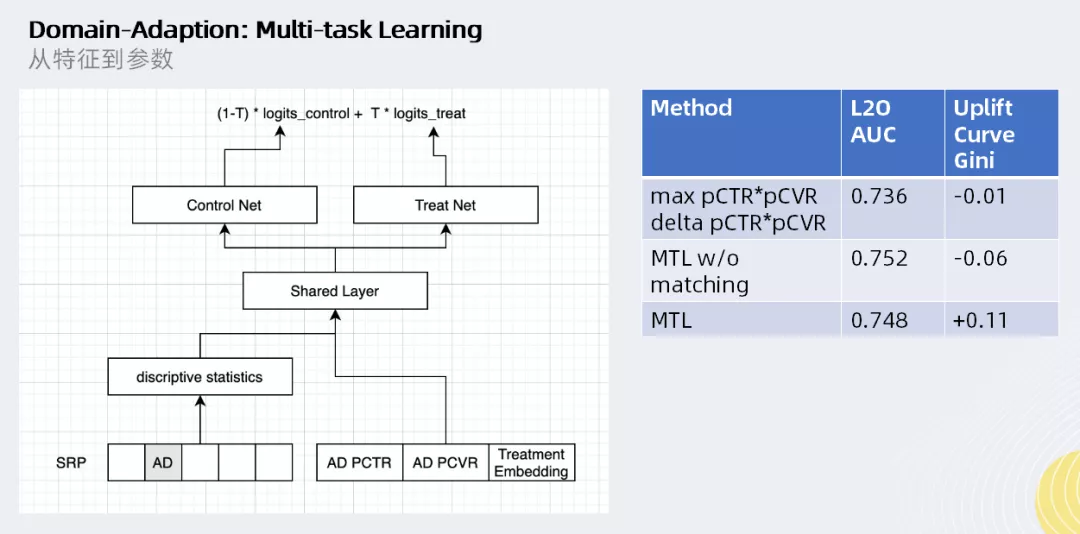
前文提到的建模方法都是将单变量treatment当作一种特征，建立基于网络结构的模型，这类基于网络结构的模型在特征权重拟合方面会受到模型结构以及数据的限制。

这里尝试换了一个思路方向，借助领域自适应中的多任务学习方法，将“是否投放广告”作为两个不同的任务（而不是一个任务中的二级特征）进行分别预估，通过建立完全不同的网络来学习“是否投放广告”产生的效果。在重采样后的样本拟合后，uplift指数可提升至0.11。然而这种方法更容易对数据分布过拟合，从上图的右表也可以看�