作者： 苏克1900

写在前面：

本文主要参考 Online Learning算法理论与实践，但该文和网上找到的资料都没有很好的给出关于模型参数w的解析解的推导过程，甚至原论文 http://www.eecs.tufts.edu/~dsculley/papers/ad-click-prediction.pdf 还有一些符号错误。所以特此写个博文记录一下自己的推导过程。

一. 什么是FTRL

首先介绍一下FTL，FTL的思想是每次找到让之前所有样本的损失函数之和最小的参数。流程如下：

初始化w

for t = 1…n

损失函数 

更新

FTRL算法就是在FTL的优化目标的基础上，加入了正则化，防止过拟合：

其中R(W) 是正则项。

二. 代理损失函数

FTRL的损失函数一般也不容易求解，这种情况下，一般需要找一个代理的损失函数。

代理损失函数需要满足以下条件：

  1. 代理损失函数比较容易求解，最好是有解析解。
  2. 代理损失函数求得的解，和原函数的解的差距越小越好

为了衡量条件2中的两个解的差距，引入regret的概念。

假设每一步用的代理函数是 

每次取：

而  是原函数的最优解，则：

表示代理函数求出来的解离真正损失函数求出来的解的损失差距。

这个损失需要满足一定的条件，Online learning才可以有效，即：

即随着训练样本的增加，代理损失函数和原损失函数求出来的参数的实际损失值差距越来越小。

三. 代理损失函数怎么选

如果  是凸函数，我们可以用下面的代理损失函数:

其中  是  的 次梯度（如果  是可导的，次梯度就是梯度）。  满足：

为了产生稀疏的解，我们可以加入L1正则项：

只要  是凸函数，上面的代理函数一定满足：

四. 怎么得出w的解析解

取只和w相关的部分：

1.当求得的w是大于等于0的时候：

其中  ，另上述偏导数等于0，可得：

所以：

因为我们现在是讨论w>=0的解，而  大于0（  大于0），所以当：

时， 才符合我们的要求

而  大于0。

令：

当 

=0时，  是肯定大于0的， 即不符合我们的要求。

：

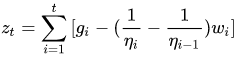当  <0时，要满足  ，即  ，即  ，

所以有：

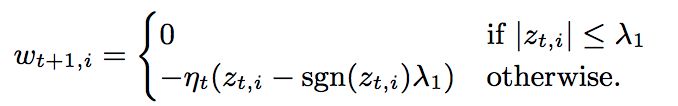
因为此时 

2.当求得的w是小于0的时候：

令偏导数等于0，可得：

因为我们现在是讨论w<0的解，而  大于0（  大于0），所以当：

时， 才符合我们的要求

而  大于0。

令  ：

当  <=0时，  是肯定小于0的， 即不符合我们的要求。

当 

0时，要满足  ，即  ，即  ，

所以有：

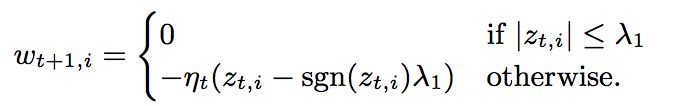
因为此时 

五. 为什么选择这个代理损失函数

参考 在线学习算法FTRL-Proximal原理 - 雪伦的专栏 - CSDN博客

重点是为什么说第一项是对损失函数的一个估计呢：

本人暂时说一个牵强的解释(g是f的梯度)：

根据泰勒展开公式：  ，如果  ，则：

就有了上述截图中类似的表达式子。

六. 遗留问题

  1. 如果  不是凸函数，我们怎么选代理损失函数？
  2. 什么是次梯度
  3. 为什么只要  是凸函数，上面的代理函数一定满足：

未完待续。。。。

参考链接：

[Online Learning算法理论与实践](https://zshipu.com/t?url=https%3A%2F%2Flink.zhihu.com%2F%3Ftarget%3Dhttps%253A%2F%2Ftech.meituan.com%2Fonli