作者：Eric He

编译：ronghuaiyang

导读: 这是Rocketmiles的搜索排名序列的第二部分。

Why we chose LambdaMART for our hotel ranking model

Part 2 of Rocketmiles’ search result ranking series

Eric He

原文： https://medium.com/rocket-travel/why-we-chose-lambdamart-for-our-hotel-ranking-model-45f84e22cec

当你是一家像Rocketmiles这样的电子商务公司时，提供无缝的购买体验是你将自己的在线商店与其他商家区分开来的为数不多的方法之一。这种体验的核心是 搜索排名算法，它选择将最好的产品放在首位。在Rocketmiles，我们部署了一个机器学习排名系统，它根据历史浏览数据学习最优的排名模式，并根据个人的偏好进行个性化调整。

在本文中，我们将深入讨论我们选择的模型：LambdaMART，这是10年前在一篇Microsoft research paper中首次讨论过的梯度提升模型。这篇文章的结构是这样的：

  1. 提升(简而言之)：利用梯度提升树的理论和实际效益

  2. LambdaMART是如何工作的？Pairwise学习，NDCG调整权重，解决表现偏差

  3. 将LambdaMART对“期望盈利能力”进行排序

  4. 关于特征工程的一些讨论

  5. 为什么不是隐语义模型？

这篇文章延续了之前的一篇文章， 酒店排名模型中的商业价值度量，它分析了模型的业务价值。

LambdaMART的优点

我们选择LambdaMART的核心原因是：

  • 灵活的数据输入。作为一个梯度提升树，LambdaMART接受任何浮点数据作为输入，允许缺失值，不需要数据标准化。只有类别变量不能被自动转换为浮点数，但是具有低基数的变量可以映射到整数。因此，我们唯一不能包含的数据是酒店id和用户id，因为它们的基数太高。

  • 强大的函数逼近能力。梯度提升树理论上是一个通用的函数逼近器。在实践中，这不会是真的，但梯度提升树的性能仍几乎无与伦比，只要特征集可以对于因变量可以形成有意义的描述。

  • 易于实现。 xgboost 包有一个高度优化的LambdaMART实现，它允许我们用一行代码在几分钟内原型化模型。

  • 有意义的得分函数。下一节将解释，模型得分可以通过一个softmax或指数函数来表示一家酒店相对于另一家酒店的预订可能性。这让我们能够根据酒店的预期盈利能力对它们进行有意义的重新排序。

  • 可解释的预测。该模型做出的每一个预测都可以用SHAP值来解释，我们在前一篇文章中提到过。

如果不首先理解LambdaMART在做什么，就很难扩展这些要点，所以我们将简要地介绍一下模型的结构。

对LambdaMART了解的更清楚一些

是时候把我的“去神秘化”也加到这一堆里了

因为LambdaMART方法经过了多年的改进，所以符号是不一致的，并且很大程度上集中在高效计算上，我们把这个问题留给了 xgboost。因此，我们的解释从头开始，重点放在对我们的用例很重要的核心思想上。

LambdaMART中的MART，非常简短

在它的核心，LambdaMART是一个损失函数(“Lambda”)附加到一个梯度提升森林(“MART” — 多重加法回归树)上。梯度提升森林通过训练一棵新树来预测之前出现的树的误差(损失函数的“梯度”)来改进它的预测。预测是通过将第一棵树的原始估计值与后续树的所有修正值相加而得出的。

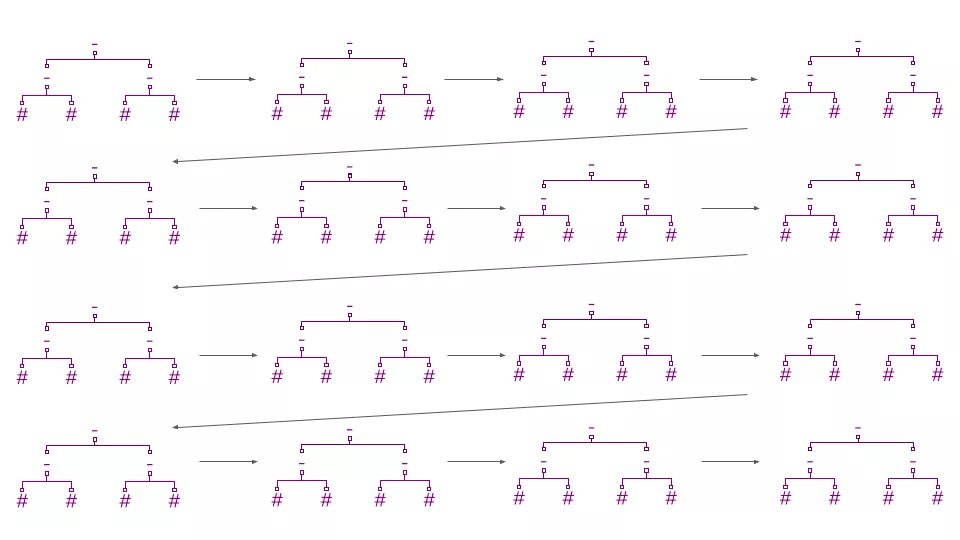
提升森林中的每一棵新树都能在集成之前提前预测出误差。

由于树不会像线性回归那样对模型函数空间施加强大的结构，LambdaMART实现良好排名的能力几乎完全取决于其“Lambda”误差的质量。由于这个原因，损失函数可以被详细的解释。

LambdaMART的损失

Lambda损失要求某些搜索结果的得分高于其他搜索结果。例如，预订的酒店应该比只被点击的酒店得分高，而被点击的酒店应该比完全被用户忽略的酒店得分高。使这些 pairwise 的比较是Lambda梯度函数的核心。

更精确地说，给定酒店和分数I，酒店和分数J，Lambda梯度估计的酒店优于酒店的概率为 σ( J-I)，其中 σ 是sigmoid函数。sigmoid通常使用e=2.7182818…，但是Lambda训练过程实际上对sigmoid的base是不变的。

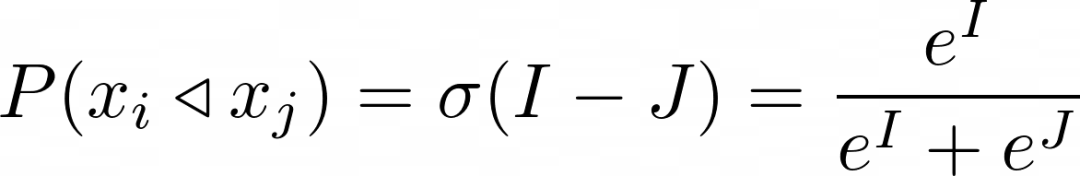
◁ 运算符表示优于，比如，a◁b 表示a优于b

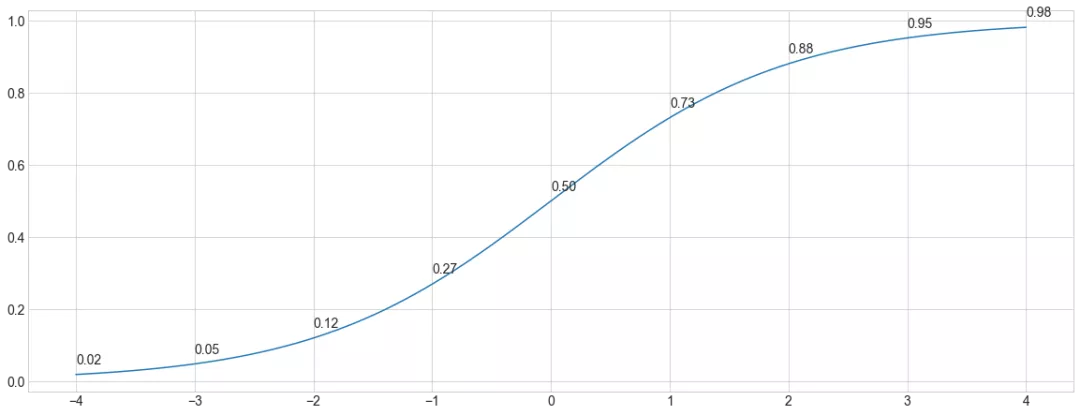
σ(x)的图

_x_i_比 _x_j_的优先的概率代表什么？以下是几种解释：

  1. 酒店_x_i_被点击或订购的次数比_x_j_大。

  2. 酒店_x_i_被选中的条件概率，假如只有_x_i_和_x_j_两个酒店，这两个酒店中只有一个被选中。

我们希望将我们估算的pairwise偏好概率与我们排名中所有酒店对( x_i, x_j)的真实偏好概率之间的距离最小化：

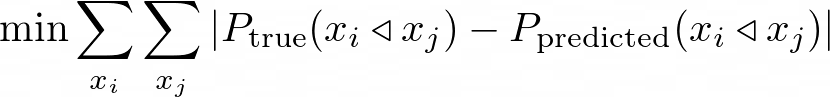
这对应的是关于x_i是否优于x_j的标准交叉熵损失。

使用这样的pairwise损失，我们就能训练出一个像样的模型。然而，我们可以考虑两个额外的效应来获得更好的性能：

并不是所有的酒店对都是一样的：例如，我们并不关心排名第340位和第341位的酒店交换模式，而是关心排名第1位和第341位的酒店交换模式。如果上面的排名更正确，那么下面的一些错误排名是可以接受的。

点击数据有偏差：排名高的结果更容易被观察到( 表示偏差)，即使被观察到了，排名高的结果也更容易被点击( 信任偏差)。考虑到这一点，排名较高的结果应该是有问题的。

我们依次来看。

使用NDCG-weighting调整listwise损失

高排名的结果相比低排名的结果的重要性通过NDCG来进行度量。下面显示了NDCG的一个表达式，其中IDCG是排序所能达到的理想或最大DCG， rel__i_是排在第i个的搜索结果的相关性标签值。

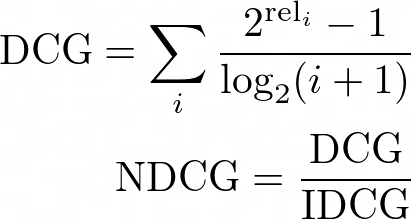
NDCG是唯一的排名指标，可以区分出两个排序中哪个是更好的一个。除此之外，它对你的直觉几乎毫无用处。随着搜索结果数量的增加，搜索请求的预期NDCG收敛到0，因此用不同的基数比较两个搜索请求的NDCGs是不合适的。

我们可以看到，当相关结果的排名较差时，DCG分数会下降，因为贡献的分数被一个对数因子打折了。NDCG为99个不相关的结果(相关标签为0)和1个相关的结果(相关标签为1)的搜索请求进行评分，下面是每一个可能的排序的相关结果图。

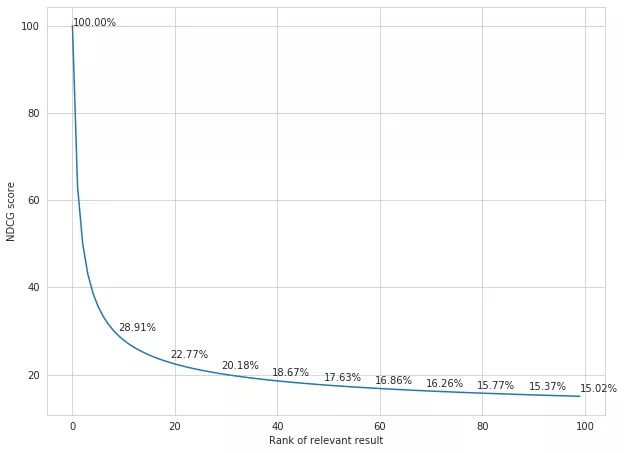
这个特殊的NDCG曲线对应于方程1/log2(x+1)

给于高排名对比低排名对更高的权重，每一对( x___i, x_j)通过ΔNDCG来加权，这个差值为NDCG分数和交换之后的NDCG分数之间的绝对差。

例如，如果相关结果排在第1位，它的NDCG值为1，而如果与排在第100位的无关结果进行交换，NDCG值为.1502。那一对排序(1, 100)的NDCG的变化为|1-0.1502|=|0.8498|。

使用反向加权来去除点击数据的偏差

表示偏差影响用户查看搜索结果的概率。如果一个搜索结果的排名靠后，那么用户看到它的几率就会降低。信任偏差会影响一个搜索结果被点击的概率，即使它被用户看过。虽然这是两种不同的效果，但它们都可以根据搜索结果的排名改变其被点击的概率。我们通过估计每个位置_i_上的两个量来衡量这种效果：

  1. 正偏好比p+(i)，搜索结果如果排在其他的位置相对于它在第i位的时候，点击率的比例。例如，如果rank 1是参考点，rank 2的正偏好比例是0.25，那么我们期望一个搜索结果在rank 2的时候被点击次数是排在rank 1的25%。在这个例子里，第一位的正偏好比例一般是1。

  2. 负偏好比p-(i)，或_倒数_是不相关的，如果它占据其他一些里程碑的排名。例如，如果rank 1是参考点，而rank 2的负偏好比是4，那么我们就会认为未被点击的rank 2的搜索结果的不相关性是未被点击的rank 1的搜索结果的4倍。

p+( i) 和 p-( i) 对于所有的排序位置i在LambdaMART训练过程中都是可迭代估计的，使用下面一组方程。其中，*L(i, j) 是原始（有偏差的）的pairwise损失函数，p 这一项是在前一次迭代中估计出来的，然后对所有的查询q和搜索结果j加起来。

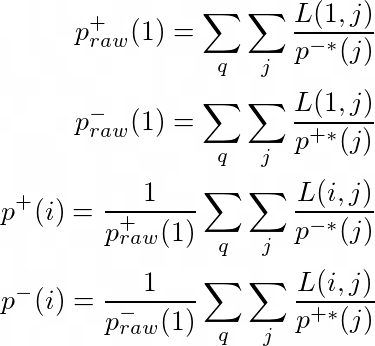
表现偏差的影响可以通过简单地用损失除以偏差来逆转。这个修正给了我们一个一致的和无偏的pairwise的损失。

把所有的组合起来

搜索结果_x_i_的Lambda梯度很简单，就是这些加权的NDCG全部加起来，就是对于每一对 ( x_i, x_j)的修正了偏差的pairwise误差。注意，使用了相同的label的结果在交换的时候在NDCG上没有变化，所以，大部分的值是0.方程如下：

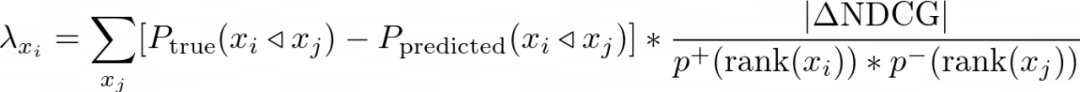
偏好概率的校准度量

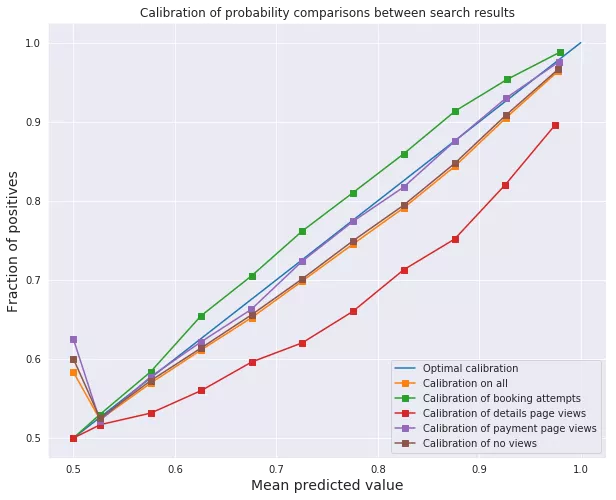
我之前说过LambdaMART估计了i优于j的偏好概率。这是一个相当强的声明，特别是当loss函数包含NDCG-weighting的时候。然而，下面的图表显示，该模型是根据经验进行了概率估计校准的。为了进行校准，酒店i，模型估计有p%的概率优于某个酒店j被选中(在x轴上)，需要实际被选中的概率为p%(在y轴上)。

原始Lambda论文还对使用Lambda梯度训练的神经网络模型参数的小扰动导致训练集上的期望NDCG较低进行了数值观察，表明该模型在拟合偏好概率的同时，联合最大化了NDCG。同时做两件事情的能力都意味着NDCG最大化和最小化的目标偏好概率损失没有强烈的相互冲突，所以我们可以鱼（校准概率）和熊掌（NDCG加权）兼得。

从pairwise偏好概率到querywise偏好分布

给定生成校准的两两偏好概率的分数，我们可以在整个搜索请求上找到一个类似的校准的偏好分布，通过多维sigmoid，称为softmax，在搜索请求的所有分数上进行操作。

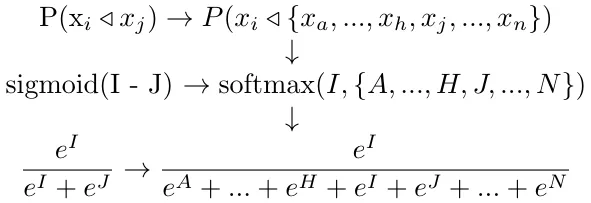
对pairwise概率的解释可以很好地扩展到querywise概率:

  1. 当给客户显示_x_a，…，x_n_时，购买_x_i_的长期比例

  2. 给定选择_x_a，…，x_n_，以条件概率_x_i_被选中

这里的逻辑相当简单：如果酒店_x_i_每被选中_i_次，酒店_x_j_被选中_j_次，酒店_x_h_被选中_h_次，那么酒店_x_i_在这三个里被选中的概率由_i / i+j+h_给出。

因为这个归一化是通过对分数进行指数运算来实现的，这只是将softmax函数和应用在任意数量的酒店上的逻辑。

我说逻辑很简单，但实际上我花了一周的时间来考虑如何计算querywise分布。想象一下我的失望，当我把数学写出来，却发现解决方案只是个softmax函数。

用几何平均来对排序目标进行组合

我们如此关注querywise概率分布的原因是，这些相关概率可以乘以酒店的盈利能力，根据预期盈利能力为我们排序：

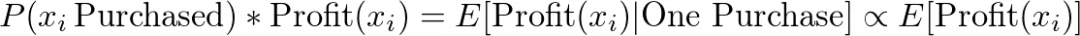
考虑到用户订购了一家酒店，最终得分代表酒店的预期利润。这个值一般与酒店的预期利润成比例。我们“希望”，通过按预期利润而非相关性排序，我们可以让客户更倾向于更有利可图的酒店，而不会对他们的转化率产生很大的负面影响。在前一篇文章中，我们实际上认为这种做法增加了排名的多样性，并可能提高转换概率，而不是降低！

将相关性与盈利能力相乘，暗示了一种更普遍的方式，我们在衡量盈利能力时明确使用了这一指标，即利润和利润率的平方根。我们提出了各种非正式的理由来说明为什么这种组合是有意义的，但是没有一个是真正严格的理由。在此，我认为，对这两个排序分数R和P的合理的组合应该对于加权几何平均是单调的，由以下公式给出：

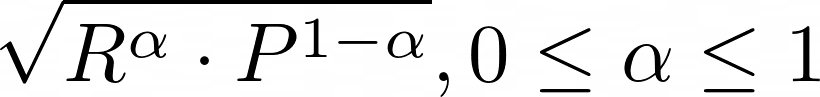
首先，请注意，利润率和利润的几何平均，就是_α_=0.5。然后相关性和盈利能力相乘和它们的几何平均数也是单调的，所以我们可以去掉平方根和α指数。

接下来，考虑两个随机向量 r 和 p 作为搜索请求的相关性和盈利能力的度量。搜索结果集{i}按照预期盈利能力r[i]p[i]来排序。假设你想要给予相关性度量 r 增加权重，以便排序系统对盈利能力不那么敏感。可以通过增加r的方差来实现，你可以通过增加α。如果 r 的(归一化)方差高于 p，那么(松散地说)它对组合排名的影响更大。

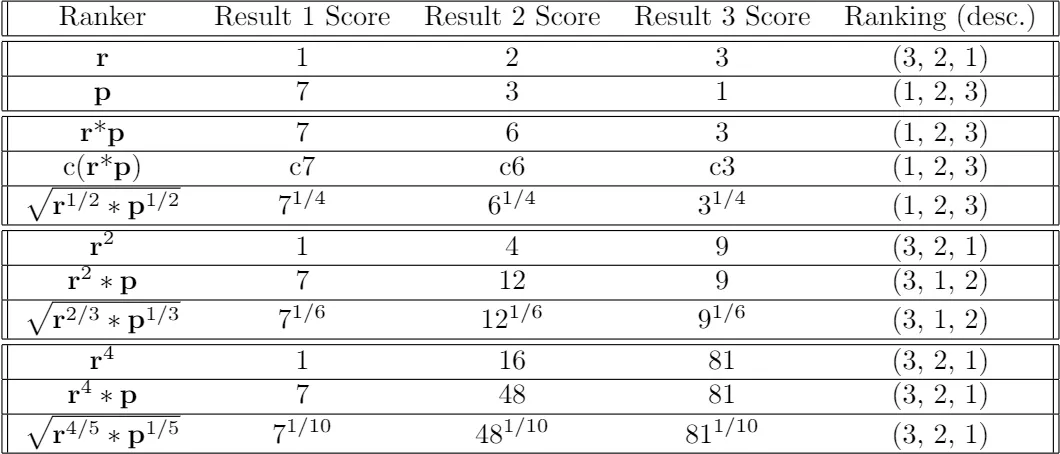
上面的图给出了不同的_α_的能力，三个搜索结果的2种不同的排序：r，排序为(3,2,1)，p排序为 (1,2,3)。对r和p归一化得到的排序为 (1,2,3)，和通过p排序是一样的。简单的乘以c和其他的r和p的单调函数也不会改变排序结果。把_α_增加到2/3，得到的排序为(3,1,2)，和使用r的排序(3,2,1)变得接近了。 α = 4/5，排序为(1,2,3)，变得和r一样了。

特征工程中的花絮

我们已经完成了对模型的训练过程，获取它的分数输出，并将其转换为预期的盈利能力的度量。然而，此度量的质量仅与提供的数据集的质量相同。我们会简要地强调一些我们所做的对模型性能有意义的特征工程的决策。

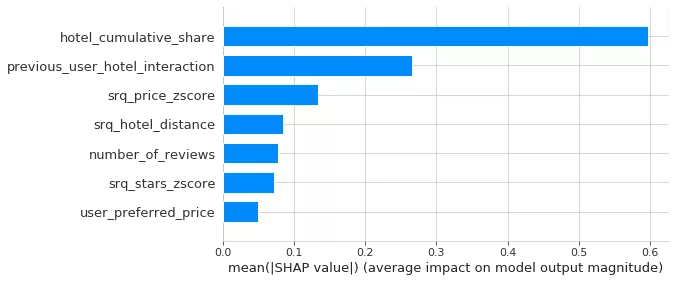
要了解更多关于这个特征重要性图的信息，请查看前面的文章中的SHAP值讨论

历史特征：过去可以给现在最有力的指导

根据我们的经验，历史特征是最难计算的，因为它们必须通过时间累积计算，而且我们在Spark中仅限于sql风格的语法。然而，努力是值得的，因为历史特征，比如 hotel_cumulative_share，衡量酒店之前被预定有多频繁，还有 previous_user_hotel_interaction，一个表示用户过去是否点击或者预定过这个酒店的类别变量。这两个对于我们的登陆用户是最重要的两个特征。使用隐语义模型把一个酒店过去的预定历史聚合成学到的“嵌入”，也许可以为模型增加重要的特征值。

根据搜索请求标准化特征：也许分类模型就可以了？

当我们根据特征在搜索请求中的相对值(例如，一个酒店价格高于平均值1.15个标准差)来描述特征时，传统的梯度提升分类器能够获得与LambdaMART接近的性能。也许这是一个声明，我们的LambdaMART模型实际上不是那好。我的观点是，表现偏差严重地降低了模型的性能，我们将在进一步的迭代中找到答案。

平滑随机用户特征：过拟合的教训

如果你读过上一篇文章，你可能还记得我和我的朋友是如何通过查看新加坡顶级酒店的排名来直观地判断LambdaMART有多好。回想一下我对模型性能的评估：

结果是，在每一个可用的测试集搜索请求中(数百个)，模型每次都将滨海湾金沙放在第一位或第二位。

在这个决定性的搜索请求中，滨海湾金沙甚至没有进入前十，排名第80位！让我们把时间倒回我拉出排名的那一刻。我看了看，耸了耸肩，然后把电脑递给我的朋友，他实际上来自新加坡，对这个地方有一点了解。她盯着电脑看了几秒钟，然后笑了起来。

什么?

“老兄，你的顶级酒店有一堆红灯区属性…”

原来，由于该用户此前曾点击过一家廉价酒店，他的 user_preferred_price 值(客户价格水平的随机估计数)很低。结果，这种模式把所有便宜的酒店都推到了顶上，而这恰好包括了大量的红灯区酒店。显然，这是模型过拟合的一个实例，因此我们将该特征改为总体的平均偏好价格_P_和用户的估计平均_U_的加权平均值，与用户的点击次数_c_加上一个偏差项_b_相对应：

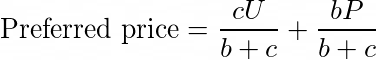
这一发现也推动了利润重排序的强劲增长，这将为排序引入一些多样性，尤其是对更便宜的用户。考虑到这两个变化，排序从主观角度看要好得多。尽管如此，如果客户愿意，我们还是有可能在现实世界中重现这个排序，我认为这是可以的。我可能对哪些酒店应该排在前面有自己的看法(比如滨海湾金沙酒店)，但我对哪些酒店……不应该排在前面的规定较少。

为什么我们不选择使用嵌入

LambdaMART不是大多数电子商务公司选择的排名模型，所以在这篇文章结束之前，我们可能应该在这里证明这个决定是正确的。最常见的方法是隐语义模型，该模型试图将客户和产品嵌入成用“隐语义”表示的属性向量。

我们不认为这些模型适合我们的用例，因为驱动酒店预订决策的重要因素并没有特别的隐藏起来。最重要的标准通常是房间的价格。紧随其后的是酒店的位置、评级、设施……所有数据字段都是即时可用的。我们不需要一个嵌入模型来发现这些“隐语义”。

事实上，使用嵌入模型甚至可能适得其反。由于嵌入模型将整个酒店封装为一个单一的向量，因此它无法适应价格、可退款性和其他对酒店价值主张至关重要的不断变化的因素。现有的推荐系统解决方案是具有这种“元数据”要求神经网络，不是我们想要的作为一个迭代的模型类型。

出于这个原因，我们选择了LambdaMART，它完全依赖于元数据。然而，放弃嵌入是一个有意义的损失。通过删除一个酒店的个体的ID，只通过它的特征来描述它，任何超出我们的特征集范围的概念都不能被模型理解，就像隐语义模型那样。例如，如果我们只有价格，LambdaMART就不可能获得酒店的品牌价值或当地的声誉，因为它们不是价格的函数。

在未来的迭代中，将单独训练的嵌入作为LambdaMART的特征，或者甚至从一个提升树切换到一个可以联合学习嵌入的神经网络，都可以极大地提高模型性能。

在数学中，“基”是一个对象的词典，它描述了同一“空间”中的其他对象。我们的“价格”等特征集构成了描述酒店空间的基。嵌入是一个更自然的基，因为在在它们上面进行操作是有意义的。当我们放弃特定于酒店的嵌入，而只根据它们的特征来描述它们时，我们就认为实体只不过是它们各部分的总和。这在多大程�