丁香园大数据NLP

引言

结合了表示学习和深度学习的图模型已经成为近些年人气最高的研究方向之一，然而令其服务于应用场景并不简单，即便线上业务能产生大量数据，如何根据数据构建符合需求的图结构依然是 强业务相关， 难以总结通用经验 的问题。在这方面，医疗信息行业有先天优势，首先从医学文献资料中就可以获取可靠的半结构化数据（就如众所周知的医疗知识图谱）此外医疗从业者的工作经验也能为我们构建图结构数据提供宝贵的先验知识。此前丁香园团队花费了大量时间精力构建图谱，同时也与医疗工作者配合，积累经验整合医疗知识，现在希望能通过图表示学习，充分发挥结构化半结构化医疗数据的潜力。

此前的文章中，笔者也介绍过以DeepWalk为代表的skip-gram模型，以及清华唐杰老师团队发表的ProNE，不过受当时认知所限，并未发觉两类方法之间的关系，本文将通过唐杰老师团队的其他工作来展示 skip-gram模型 和**矩阵分解(matrix factorization)**的关联，并讨论实践过程中与图构建和重构图表示向量有关的问题。

skip-gram模型其实也是矩阵分解

以DeepWalk为代表的 基于skip-gram 的表示模型，包括Line和node2vec，基本都能归纳为上下文采样后套用word2vec的学习模式；这类方法操作简单，大规模图数据也有对应分布式实现，且经过工业界多年验证，属于性价比极高的应用落地基线方法（如果某种追求指标的新方法不能明显超越它们，那么对应的改进思路可能就需要重新考量）。而 基于矩阵分解 的表示模型算是另一大类，不同于skip-gram可以逐步采样训练，矩阵分解需要加载整个邻接图，分布式也相对复杂，现今常见的优化思路主要是寻找可表达或近似邻接图的稀疏矩阵，并匹配基于稀疏矩阵的分解算法，例如之前介绍过的ProNE。

虽然skip-gram和matrix factorization普遍被视为两类方法，但清华唐杰老师团队通过数学分析，告诉我们 基于skip-gram的表示模型本质上也是在做矩阵分解，并尝试用矩阵分解来近似和提升skip-gram模型。

《Network Embedding as Matrix Factorization: Unifying DeepWalk, LINE, PTE, and node2vec 》

本篇的论述过程非常精彩，在第二节中分别将LINE, PTE, DeepWalk, node2vec这四个常见的skip-gram模型转换为下图中的矩阵分解形式，笔者能力有限，这里仅通过简要展示LINE和DeepWalk的推导来展示skip-gram模型到矩阵分解的跨越，PTE可视为LINE的特例，node2vec沿用了DeepWalk的思路，感兴趣的读者可自行翻阅原文学习。

1. LINE

我们知道，LINE(二阶)可以视作替换了滑动窗口的word2vec，因此二者的损失函数形式相同，从skip-gram到matrix factorization的变换就从损失函数开始

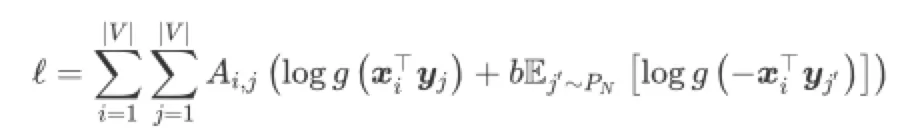
根据LINE中作者的建议，对节点j的负采样可正比于节点度数d的0.75次方，下面的公式里简化为正比于d，可以将损失函数改写为

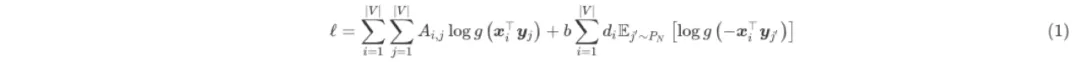
注意上式负采样中的均值部分，显然log函数的概率可以用邻接图中对应节点的度表示，即

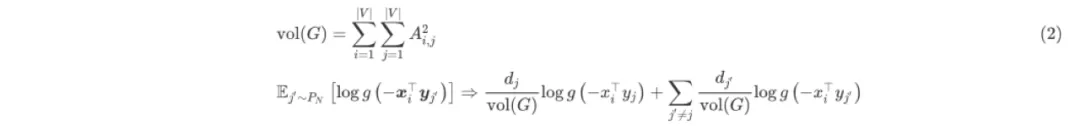
根据(1)和(2)，损失函数的每一项loss(i, j)可写为

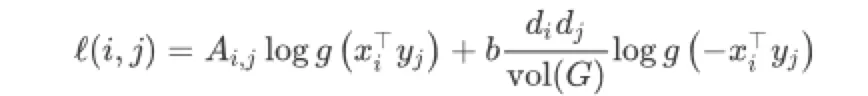
训练LINE就是最大化损失函数，所以用zi,j表示向量xy内积，对上式求导取导数为0可得

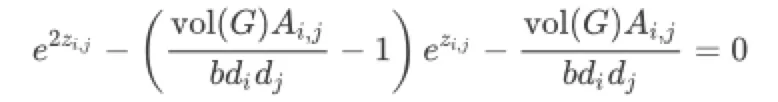
上式只存在一个基本可由图表示有效解

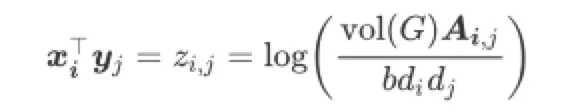
显然，将上面的解写为矩阵形式后，LINE要学习的两个Embedding参数X和Y就表现为matrix factorization的形式

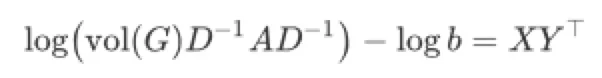
2. DeepWalk

将skip-gram转换为matrix factorization基本都是由损失函数出发，LINE非常贴近word2vec因此过程也相对容易，DeepWalk还有随机游走采样步骤，所以对应的推导也需要涵盖这一过程，下面的Skip-gram with Negative Sampling(SGNS)引用了《Neural Word Embedding as Implicit Matrix Factorization》（讨论word embedding与matrix factorization的关系）中给出的损失函数形式，下面对DeepWalk的推导基于该形式，其中矩阵D为特定采样产生的图，(W) 表示出现频率

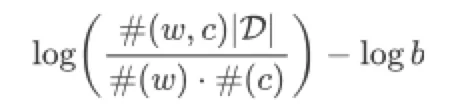
要基于上式表达DeepWalk，明显需要用邻接图D和词频率表示随机游走过程，这里作者将D划分为多个子图，每个子图代表窗口大小为r时的采样结果，由于是无向图，(w, c)共现需要考虑前向和后向两部分

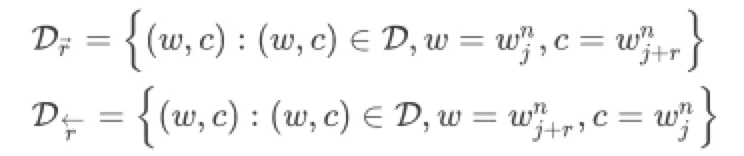
现在，基于上述表示，以及三条Theorem（证明过程请阅读原文），结合DeepWalk随机游走的SGNG损失函数可以转换为矩阵分解形式

  • Theorem 2.1：用图的形式来表述子图Dr下#(w, c)的共现频率（L为游走步长）

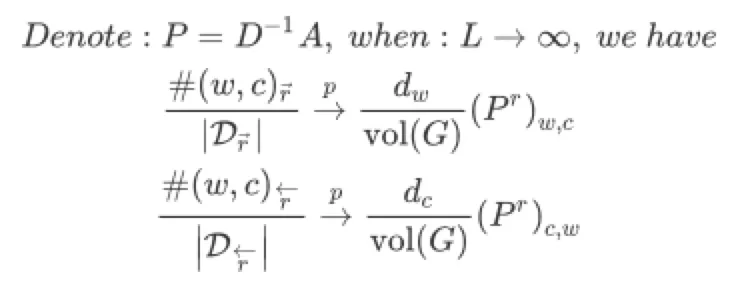
  • Theorem 2.2：说明当步长L趋于无穷时，基于完整图D的共现频率可用子图共现频率的和表示（T为最大窗口）

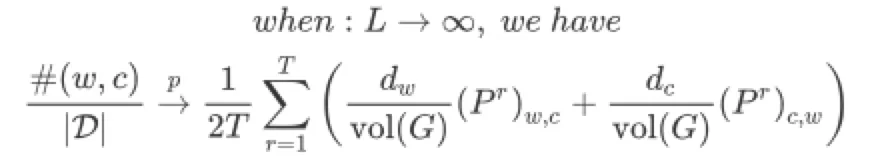
  • Theorem 2.3：基于Theorem2.1和2.2，SGNS损失函数很容易用矩阵求和的形式表达

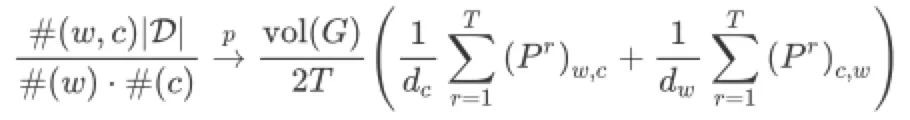
最终，将Theorem2.3改写为矩阵形式即可得（不难看出，LINE就是当T=1时的DeepWalk）

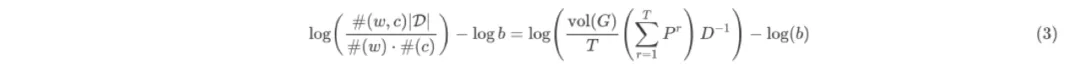
3. 矩阵分解框架NetMF

文章3.1小节对矩阵分解形式的DeepWalk做谱分析，揭示了DeepWalk与Graph Laplacian的关系，并给出有关特征值的性质和界，这里不再赘述，直接来到作者提出的框架（基于公式(3)右式），将待分解矩阵记为M，即：

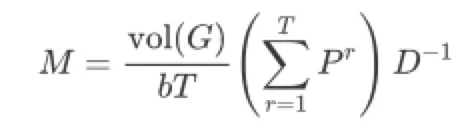
  • 小窗口T

较小的窗口T对应较低的运算量，此时应用NetMF不必考虑对M近似，对应原文的算法3，先计算每个窗口下的P，代入计算出M，最后应用奇异值分解；此处第3步的 M'=max(M, 1) 是为了消除 log(0) 的情况，同时log(1) = 0也能让矩阵稠密程度降低

  • 大窗口T

窗口尺寸T上升会令计算复杂度显著提高，因此作者提出先用特征分解，取top-h的特征对作为M的近似，提升M的稀疏程度

至此便是本篇的主体内容，将应用多年的skip-gram模型统一为矩阵分解，意味着我们有机会应用更多图算法去改进skip-gram，同一个团队在第二年就展示了应用图稀疏化方法提升框架性能的工作NetSMF。

《NetSMF: Large-Scale Network Embedding as Sparse Matrix Factorization》

NetMF慢主要还是因为 输入矩阵M不够稀疏，本文利用图谱稀疏化技术（graph sparsification technique）构造M的稀疏近似矩阵，并用随机奇异值分解（RSVD）生成稀疏图的对应Embedding，为了与本文的符号一致，这里重新给出DeepWalk的矩阵分解形式以及M在本文里的表示

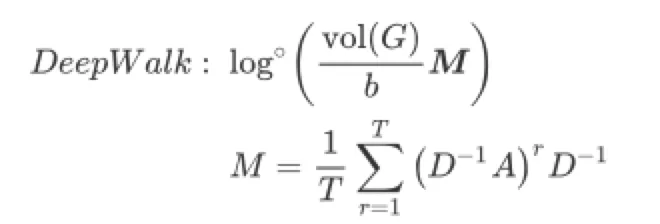
显然图谱稀疏化是本文的核心，思路是基于原图的连接关系，重新采样生成新的边和边权重，下面的算法1是NetSMF的整体流程（这里跳过了图谱相似的定义以及随机游走多项式的谱稀疏性定理，他们共同说明了在 特定复杂度 内构造的图与原图的 谱相似 程度，感兴趣的读者可参阅原文3.1节）

其中第5步对应边采样算法（算法2）：根据真实挑选的边e=(u, v)，在u和v的特定范围邻居中采样新的节点(u0, ur)作为新边，并通过新边间通路长度算得新边权重

第10步的RSVD分解会将原输入矩阵映射到低维空间，这将进一步提升整体框架运算效率；此外，作者还分析了NetSMF的并行化能力，并描述了边采样，稀疏矩阵构造，RSVD三个关键部分的并行实现思路；文中的效率实验表明NetSMF对比DeepWalk和NetMF有大幅提升。

不过这还不够，如今工业界应用图表示的场景恐怕都是千万节点起步，ProNE继续沿着NetMF的思路，在matrix factorization的框架上找到了更快更巧妙的技术，特别是第二部分，对分解产生的Embedding做谱传播，图傅立叶变换会将输入投影到谱空间，投影过程中拉普拉斯矩阵的特征值会缩放输入矩阵，并且该特征值与输入图矩阵本身的内聚程度有关，因此在谱传播过程中，第一部分对图表示向量将依特征值大小被传播到更局部或全局部分。

应用图表示学习时的障碍

笔者之前对医疗文本中的实体词和内部医学知识词库做原子词表示时用了ProNE，结果都很不错，然而将相似的思路应用到其他文本数据时结果很糟糕，举个例子：麻疹和荨麻疹其实是两种病，但多数人其实分不清它们，医学科普文章又经常将二者放在一起比较，所以滑动窗口采样出的上下文非常接近，笔者考虑把word2vec的滑动窗口视为边采样，再结合原子词表示的实体边采样方式，由二者共同构成词表的邻接矩阵，希望这样学习到的词向量表示有更强的实体倾向性（例如二者的传染源不同，临床症状不同）。

我们猜测，如果词表构成内聚程度强，或数据本身就存在结构化/半结构化结构，对应图的表意就会相对明确，自然用简单的构图策略就可以产生符合期望的图，而对更泛的语料，大量平凡用语产生的上下文会淡化重点词汇间的关系，这样简单的构图策略就无法表达我们的目标意图；所以，应该设计更复杂的构图策略，并为图结构赋予更复杂的信息，GNN在推荐系统等场景中发展出的异质网络就是很好的学习对象，来自阿里和唐杰老师团队的GATNE就融合了不同类型的边，以求学习复杂场景下的表示向量。

《Representation Learning for Attributed Multiplex Heterogeneous Network》

虽说是更复杂的图结构，但GATNE的思路非常直观，如下图所示，除了常规通过节点邻接关系学习到的 Base Embedding，节点间的边可能蕴含不同的属性，因此完整的图结构是由不同类别的边连接而成的子图之和，这里需要学习各类边的 Edge Embedding，每个节点最终的向量表示就是对应 Edge 和 Base 表示的组合，因为线性组合无法体现节点之间及不同类边的影响，因而在concat操作后还会用注意力机制为不同表示加权

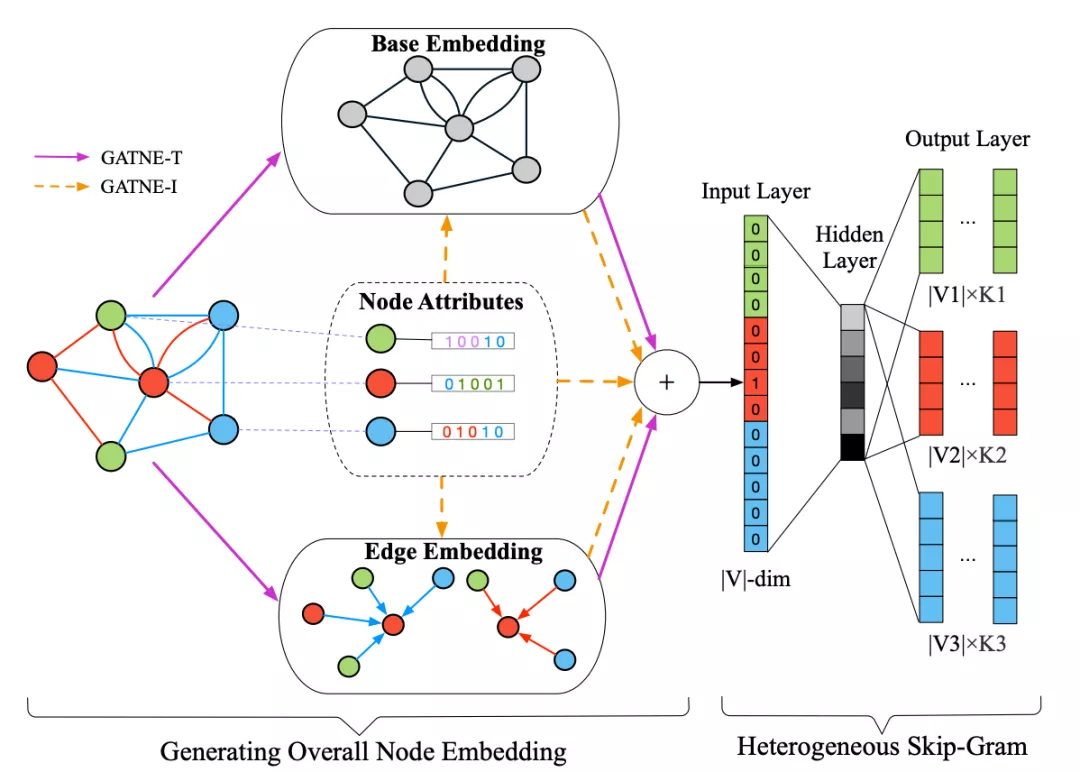
本文还分别讨论了 Transductive 和 Inductive 两种情况（对应 GATNE-T 和 GATNE-I）；无疑 Transductive 更简单，重点放在 Edge 表示学习即可，对应操作就是以 特定类别的边产生的邻居的聚合 作为该节点对应此类边的表示向量；而 GATNE-I 需要考虑新数据加入， Base 向量就借用GraphSAGE的邻居聚合思想， Edge 表示由于新节点加入会改变整体结构，因此不能通过 GATNE-T 的邻居聚合实现，这里通过训练由 Base 到 Edge 的转换函数实�