来源：Datawhale

寄语：本文介绍了 SVM 的理论，细致说明了“间隔”和“超平面”两个概念；随后，阐述了如何最大化间隔并区分了软硬间隔 SVM；同时，介绍了 SVC 问题的应用。最后，用 SVM 乳腺癌诊断经典数据集，对 SVM 进行了深入的理解。

支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机。

SVM 的的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM 的的学习算法就是求解凸二次规划的最优化算法。

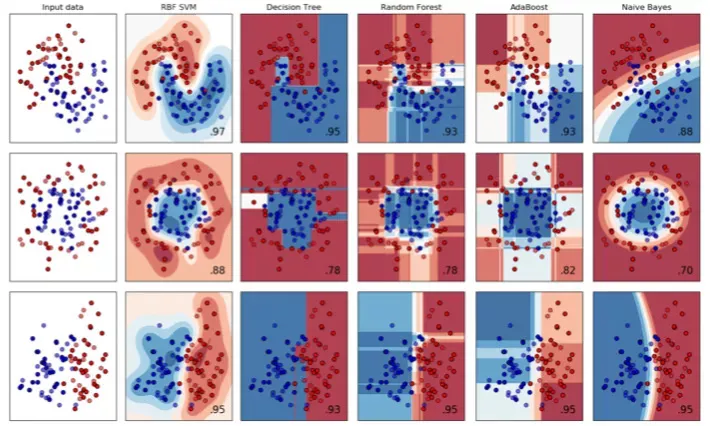
下图为 SVM 的分类效果显示，可以发现，不管是线性还是非线性，SVM 均表现良好。

学习框架

SVM 理论

支持向量机(Support Vector Machine：SVM)的目的是用训练数据集的间隔最大化找到一个最优分离超平面。

下边用一个例子来理解下间隔和分离超平面两个概念。现在有一些人的身高和体重数据，将它们绘制成散点图，是这样的：

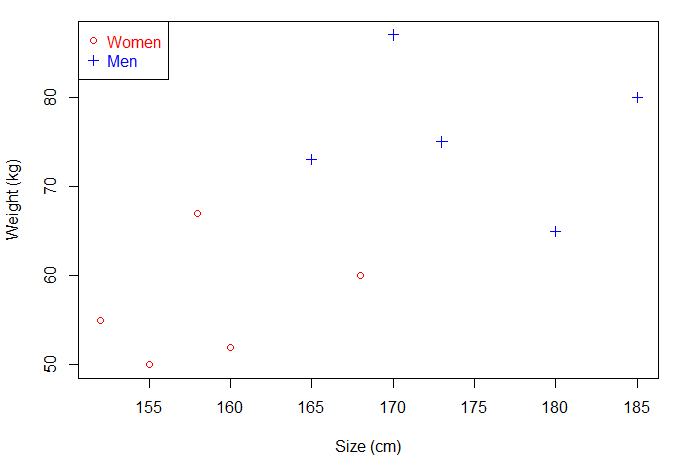
如果现在给你一个未知男女的身高和体重，你能分辨出性别吗？直接将已知的点划分为两部分，这个点落在哪一部分就对应相应的性别。那就可以画一条直线，直线以上是男生，直线以下是女生。

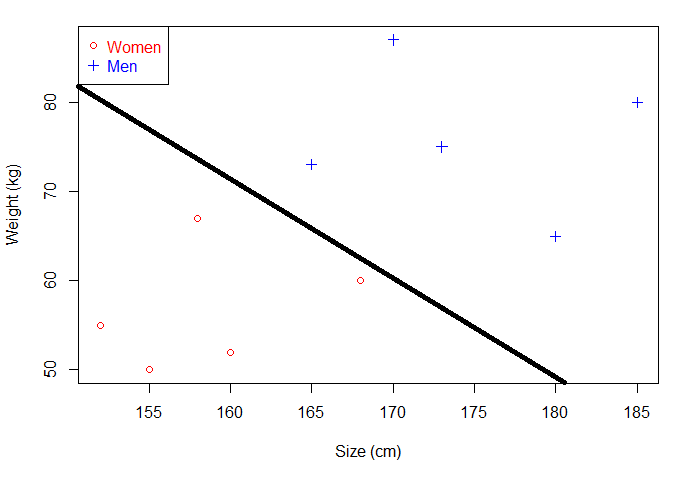
问题来了，现在这个是一个二维平面，可以画直线，如果是三维的呢？该怎么画？我们知道一维平面是点，二维平面是线，三维平面是面。

对的，那么注意，今天的第一个概念：超平面是平面的一般化：

  • 在一维的平面中，它是点
  • 在二维的平面中，它是线
  • 在三维的平面中，它是面
  • 在更高的维度中，我们称之为超平面

注意：后面的直线、平面都直接叫超平面了。

继续刚才的问题，我们刚才是通过一个分离超平面分出了男和女，这个超平面唯一吗？很明显，并不唯一，这样的超平面有若干个。

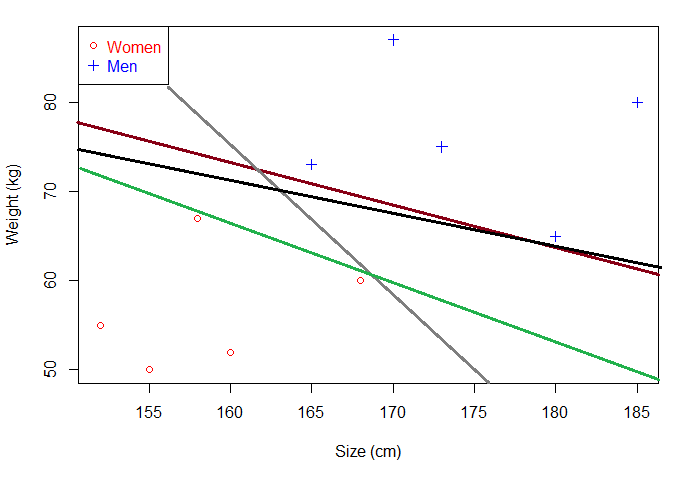
那么问题来了，既然有若干个，那肯定要最好的，这里最好的叫最优分离超平面。如何在众多分离超平面中选择一个最优分离超平面？下面这两个分离超平面，你选哪个？绿色的还是黑色的？

对，当然是黑色的，可是原理是什么？很简单，原理有两个，分别是：

  • 正确的对训练数据进行分类
  • 对未知数据也能很好的分类

黑色的分离超平面能够对训练数据很好的分类，当新增未知数据时，黑色的分离超平面泛化能力也强于绿色。深究一下，为什么黑色的要强于绿色？原理又是什么？

其实很简单：最优分离超平面其实是和两侧样本点有关，而且只和这些点有关。怎么理解这句话呢，我们看张图：

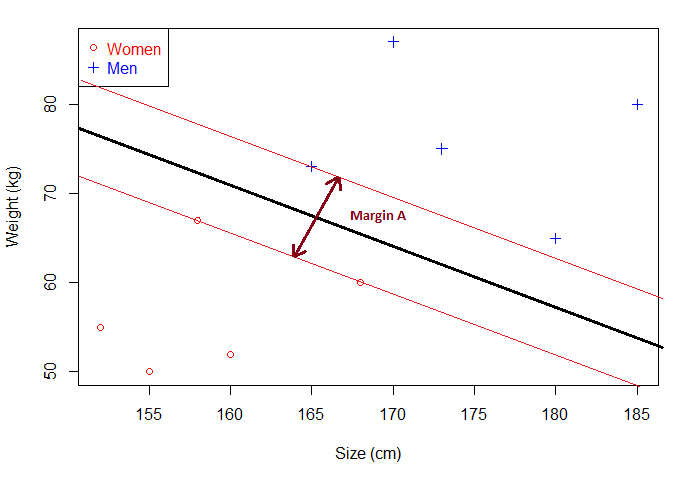
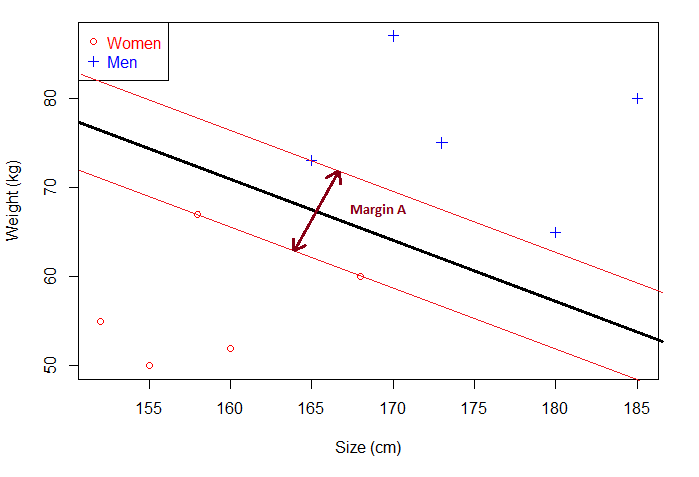
其中当间隔达到最大，两侧样本点的距离相等的超平面为最优分离超平面。注意，今天的第二个概念：对应上图，Margin 对应的就是最优分离超平面的间隔，此时的间隔达到最大。

一般来说，间隔中间是无点区域，里面不会有任何点（理想状态下）。给定一个超平面，我们可以就算出这个超平面与和它最接近的数据点之间的距离。那么间隔（Margin）就是二倍的这个距离。

如果还是不理解为什么这个分离超平面就是最优分离超平面，那你在看这张图。

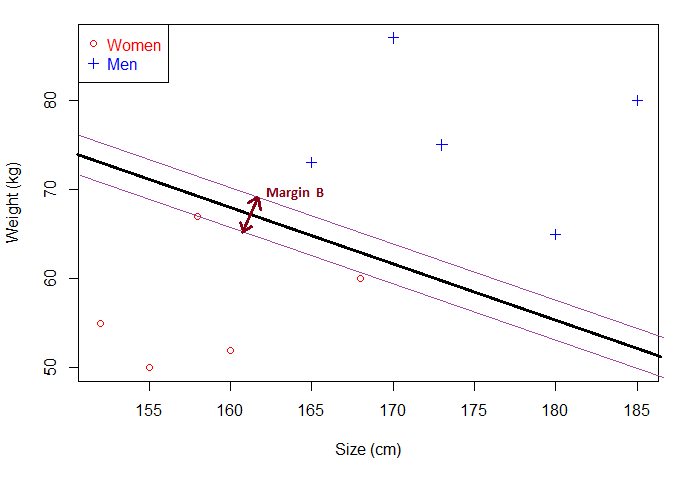在这张图里面间隔 MarginB 小于上张图的 MarginA。当出现新的未知点，MarginB 分离超平面的泛化能力不如 MarginA，用 MarginB 的分离超平面去分类，错误率大于 MarginA

总结一下

支持向量机是为了通过间隔最大化找到一个最优分离超平面。在决定分离超平面的时候，只有极限位置的那两个点有用，其他点根本没有大作用，因为只要极限位置离得超平面的距离最大，就是最优的分离超平面了。

如何确定最大化间隔

如果我们能够确定两个平行超平面，那么两个超平面之间的最大距离就是最大化间隔。看个图你就都明白了：

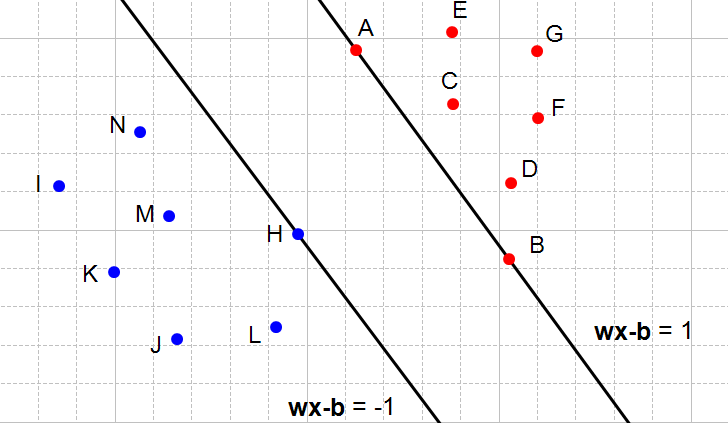
左右两个平行超平面将数据完美的分开，我们只需要计算上述两个平行超平面的距离即可。所以，我们找到最大化间隔：

  • 找到两个平行超平面，可以划分数据集并且两平面之间没有数据点
  • 最大化上述两个超平面
1. 确定两个平行超平面

怎么确定两个平行超平面？我们知道一条直线的数学方程是：y-ax+b=0，而超平面会被定义成类似的形式：

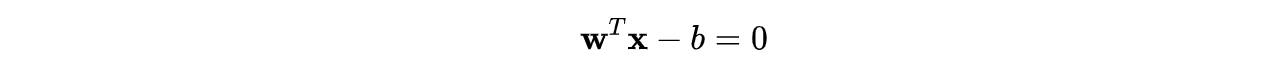
推广到 n 维空间，则超平面方程中的 w、x 分别为：

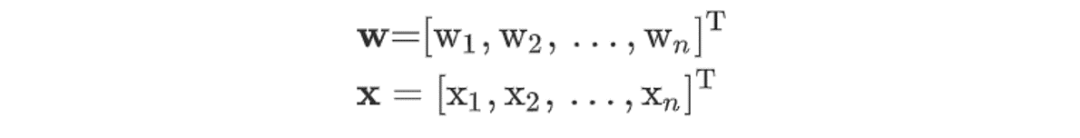如何确保两超平面之间没有数据点？我们的目的是通过两个平行超平面对数据进行分类，那我们可以这样定义两个超平面。

对于每一个向量x_i：满足：

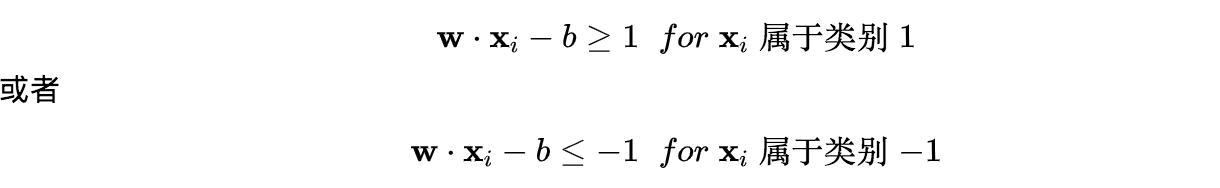
也就是这张图：所有的红点都是 1 类，所有的蓝点都是 −1 类。

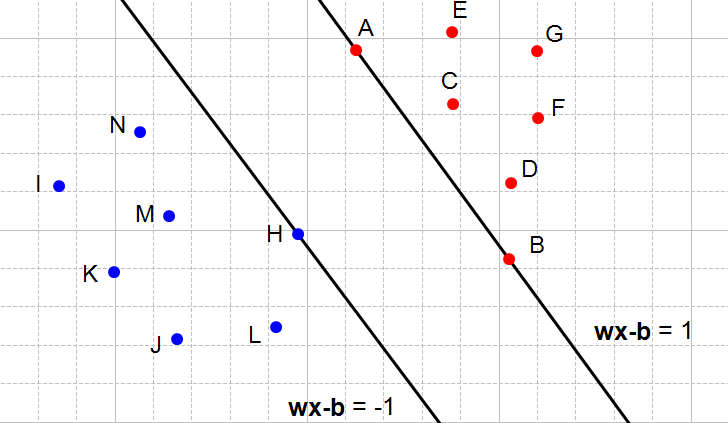
整理一下上面的两个超平面：

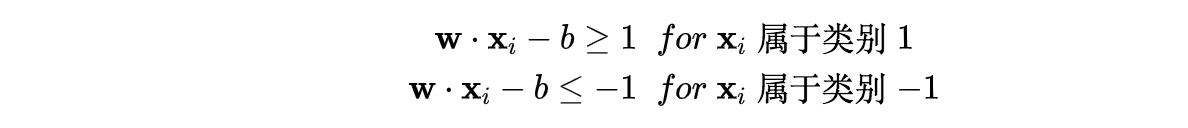
不等式两边同时乘以 y_i，-1 类的超平面y_i=-1，要改变不等式符号，合并后得

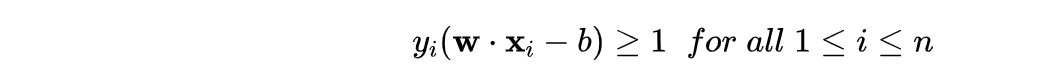
ok，记住上面的约束条件。

2. 确定间隔

如何求两个平行超平面的间隔呢？我们可以先做这样一个假设：

  • h_0 是满足约束 w \cdot x_i -b=1 的超平面
  • h_1 是满足约束 w \cdot x_i -b=-1 的超平面
  • x_0是h_0上的一点

则x_0到平面h_1的垂直距离m就是我们要的间隔。

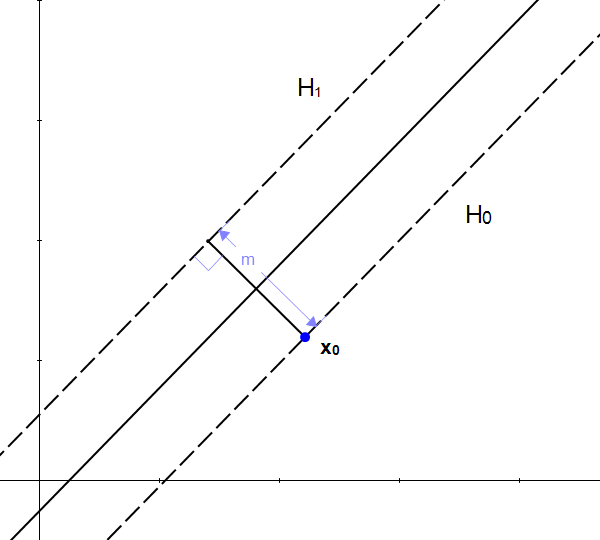
这个间隔是可以通过计算出来的，推导还需要一些步骤，直接放结果了就：

m=\frac{2}{ \lVert w \lVert }

其中 ||w|| 表示 w 的二范数，求所有元素的平方和，然后在开方。比如，二维平面下：

\lVert w \lVert = \sqrt{w^2_1 + w^2_2}

可以发现，w 的模越小，间隔 m 越大

3. 确定目标

我们的间隔最大化，最后就成了这样一个问题：

在约束条件对于的情况下 y_i(w \cdot x_i-b) \geq 1（对于i=1,…,n）的情况下

找到使 \lVert w \lVert 最小的w,b

了其中 w 和 b，我们的最优分离超平面就确定了，目的也就达到了。

上面的最优超平面问题是一个凸优化问题，可以转换成了拉格朗日的对偶问题，判断是否满足 KKT 条件，然后求解。上一句话包含的知识是整个 SVM 的核心，涉及到大量的公式推导。

此处略过推导的步骤，若想了解推导过程可直接百度。你只需要知道它的目的就是为了找出一个最优分离超平面。就假设我们已经解出了最大间隔，找到了最优分离超平面，它是这样的：

除去上面我们对最大间隔的推导计算，剩下的部分其实是不难理解的。从上面过程，我们可以发现，其实最终分类超平面的确定依赖于部分极限位置的样本点，这叫做支持向量。

由于支持向量在确定分离超平面中起着决定性作用，所有将这类模型叫做支持向量机。

我们在上面图中的点都是线性可分的，也就是一条线（或一个超平面）可以很容易的分开的。但是实际情况不都是这样，比如有的女生身高比男生高，有的男生体重比女生都轻，像这种存在噪声点分类，应该怎么处理？

针对样本的 SVM

1. 硬间隔线性 SVM

上面例子中提到的样本点都是线性可分的，我们就可以通过分类将样本点完全分类准确，不存在分类错误的情况，这种叫硬间隔，这类模型叫做硬间隔线性 SVM。

2. 软间隔线性 SVM

同样的，可以通过分类将样本点不完全分类准确，存在少部分分类错误的情况，这叫软间隔，这类模型叫做软间隔线性 SVM。

不一样的是，因为有分类错误的样本点，但我们仍需要将错误降至最低，所有需要添加一个惩罚项来进行浮动，所有此时求解的最大间隔就变成了这样：

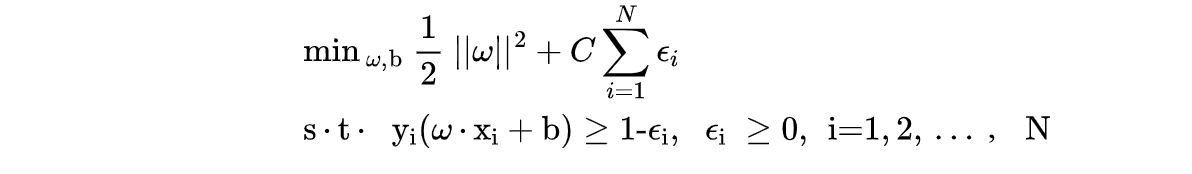
硬间隔和软间隔都是对线性可分的样本点进行分类，那如果样本点本身就不线性可分？举个例子：下面这幅图

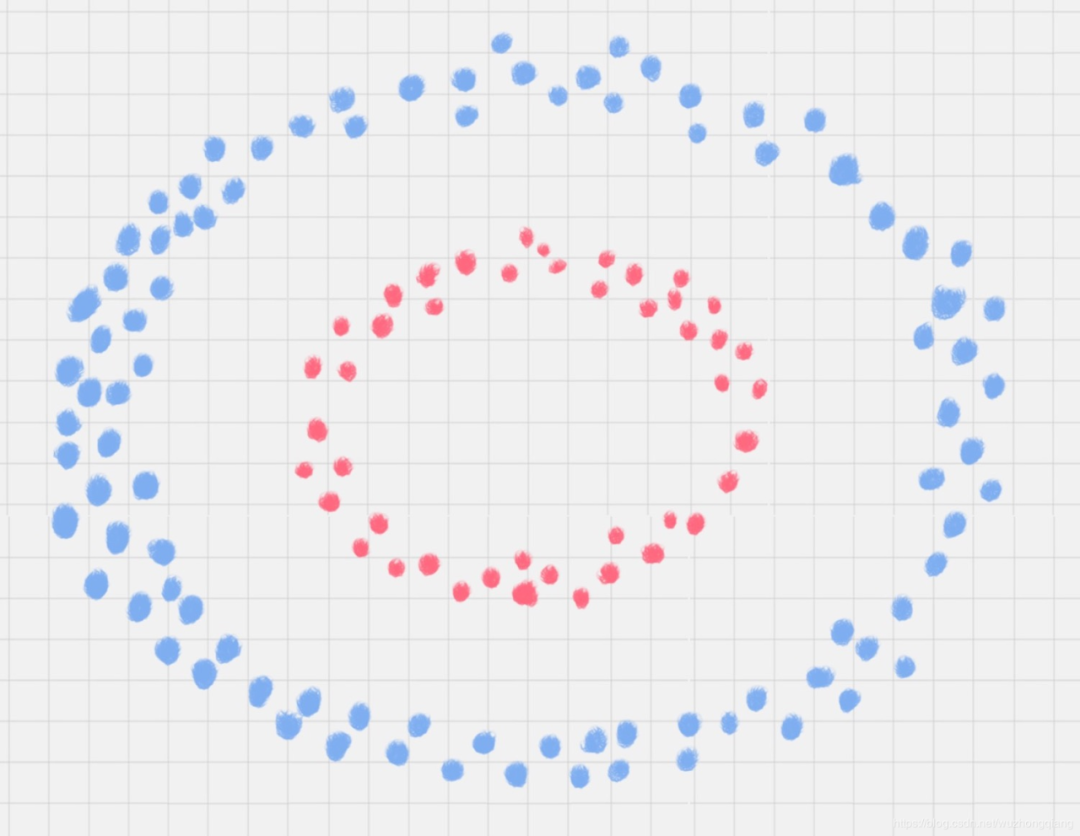
样本点并不是线性可分的，这种问题应该怎么处理呢？解决这个问题之前，先看一下这个小短视频：

视频中是将平面中的样本点映射到三维空间中，使用一个平面将样本线性可分。

所以我们需要一种方法，可以将样本从原始空间映射到一个更高纬的空间中，使得样本在新的空间中线性可分，即：核函数。在非线性 SVM 中，核函数的选择关系到 SVM 的分类效果。

幸好的是，我们有多种核函数：线性核函数、多项式核函数、高斯核函数、sigmoid 核函数等等，甚至你还可以将这些核函数进行组合，以达到最优线性可分的效果

核函数了解到应该就差不多了，具体的实现我们在下一节的实战再说。

多分类 SVM

前面提到的所有例子最终都指向了二分类，现实中可不止有二分类，更多的是多分类问题。那么多分类应该怎么分呢？有两种方法：一对多和一对一。

1. 一对多法

一对多法讲究的是将所有的分类分成两类：一类只包含一个分类，另一类包含剩下的所有分类

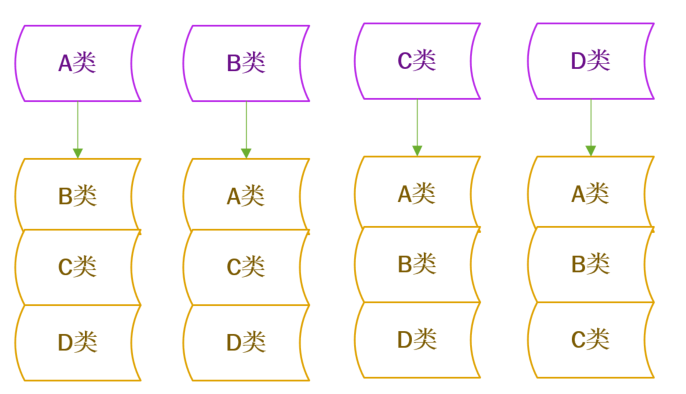
举个例子：现在有 A、B、C、D 四种分类，根据一对多法可以这样分：

  • ①：样本 A 作为正集，B、C、D 为负集
  • ②：样本 B 作为正集，A、C、D 为负集
  • ③：样本 C 作为正集，A、B、D 为负集
  • ④：样本 D 作为正集，A、B、C 为负集

该方法分类速度较快，但训练速度较慢，添加新的分类，需要重新构造分类器。

2. 一对一法

一对一法讲究的是从所有分类中只取出两类，一个为正类一个为父类

再举个例子：现在有 A、B、C 三种分类，根据一对一法可以这样分：

  • ①分类器：样本 A、B
  • ②分类器：样本 A、C
  • ③分类器：样本 B、C

该方法的优点是：当新增一类时，只需要训练与该类相关的分类器即可，训练速度较快。缺点是：当类的种类 K 很多时，分类器个数 K(K-1)/2 会很多，训练和测试时间较慢。

SVC，Support Vector Classification

我们知道针对样本有线性 SVM 和非线性 SVM。同样的在 sklearn 中提供的这两种的实现，分别是：LinearSVC 和 SVC。

SVC : Support Vector Classification 用支持向量机处理分类问题

SVR : Support Vector Regression 用支持向量机处理回归问题

1. SVC 和 LinearSVC

LinearSVC 是线性分类器，用于处理线性分类的数据，且只能使用线性核函数。SVC 是非线性分类器，即可以使用线性核函数进行线性划分，也可以使用高维核函数进行非线性划分。

2. SVM 的使用

在 sklearn 中，一句话调用 SVM，

from sklearn import svm

主要说一下 SVC 的创建，因为它的参数比较重要

model = svm.SVC(kernel='rbf', C=1.0, gamma=0.001)

分别解释一下三个重要参数：\* kernel 代表核函数的选择，有四种选择，默认 rbf（即高斯核函数）

  • 参数 C 代表目标函数的惩罚系数，默认情况下为 1.0
  • 参数 gamma 代表核函数的系数，默认为样本特征数的倒数

其中 kernel 代表的四种核函数分别是：

  • linear：线性核函数，在数据线性可分的情况下使用的
  • poly：多项式核函数，可以将数据从低维空间映射到高维空间
  • rbf：高斯核函数，同样可以将样本映射到高维空间，但所需的参数较少，通常性能不错
  • sigmoid：sigmoid 核函数，常用在神经网络的映射中

SVM 的使用就介绍这么多，来实战测试一下。

经典数据集实战

1. 数据集

SVM 的经典数据集：乳腺癌诊断。医疗人员采集了患者乳腺肿块经过细针穿刺 (FNA) 后的数字化图像，并且对这些数字图像进行了特征提取，这些特征可以描述图像中的细胞核呈现。通过这些特征可以将肿瘤分成良性和恶性。

本次数据一共 569 条、32 个字段，先来看一下具体数据字段吧：

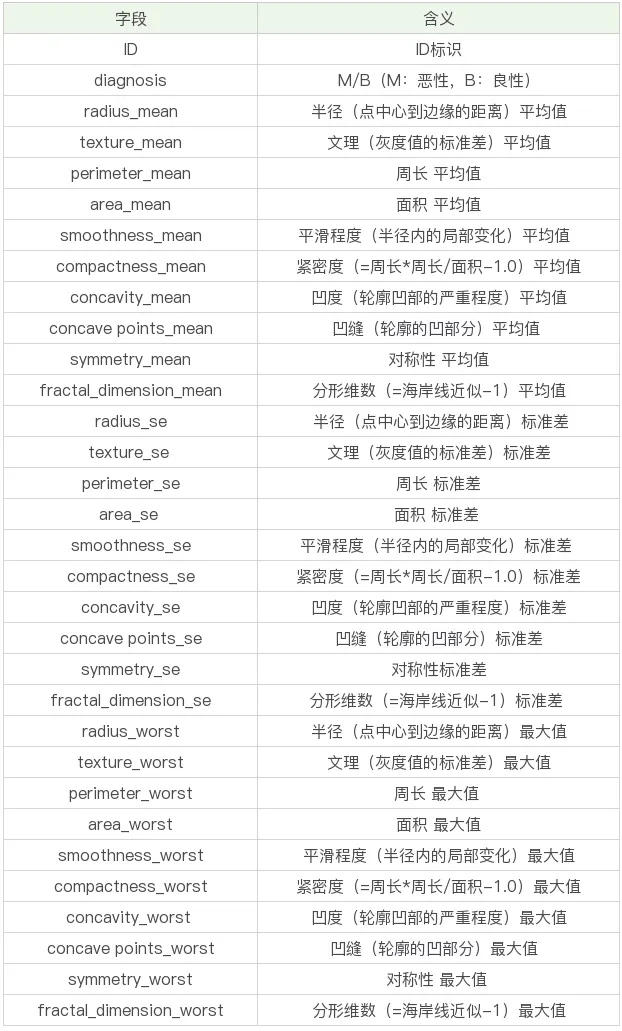
其中 mean 结尾的代表平均值、se 结尾的代表标准差、worst 结尾代表最坏值（这里具体指肿瘤的特征最大值）。所有其实主要有 10 个特征字段，一个 id 字段，一个预测类别字段。我们的目的是通过给出的特征字段来预测肿瘤是良性还是恶性。

2. 数据 EDA

EDA:Exploratory Data Analysis 探索性数据分析，先来看数据的分布情况：

df_data.info()

一共 569 条、32 个字段。32 个字段中 1 个 object 类型，一个 int 型 id，剩下的都是 float 类型。另外：数据中不存在缺失值。

大胆猜测一下，object 类型可能是类别型数据，即最终的预测类型，需要进行处理，先记下。再来看连续型数据的统计数据：

df_data.describe()

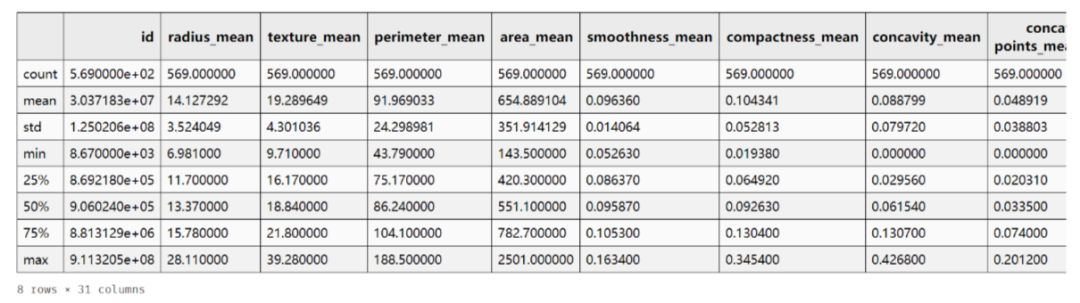
好像也没啥问题（其实因为这个数据本身比较规整），可直接开始特征工程吧。

3. 特征工程

首先就是将类别数据连续化


"""2. 类别特征向量化"""
le = preprocessing.LabelEncoder()
le.fit(df_data['diagnosis'])
df_data['diagnosis'] = le.transform(df_data['diagnosis'])

再来观察每一个特征的三个指标：均值、标准差和最大值。优先选择均值，最能体现该指特征的整体情况。

"""3. 提取特征"""
 # 提取所有mean 字段和label字段
df_data_X = df_data.filter(regex='_mean')
df_data_y = df_data['diagnosis']

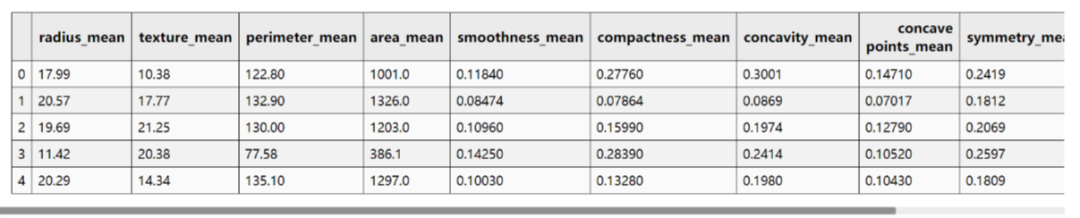
现在还有十个特征，我们通过热力图来看一下特征之间的关系。


#热力图查看特征之间的关系
sns.heatmap(df_data[df_data_X.columns].corr(), linewidths=0.1, vmax=1.0, square=True,
            cmap=sns.color_palette('RdBu', n_colors=256),
            linecolor='white', annot=True)
plt.title('the feature of corr')
plt.show()

热力图是这样的：

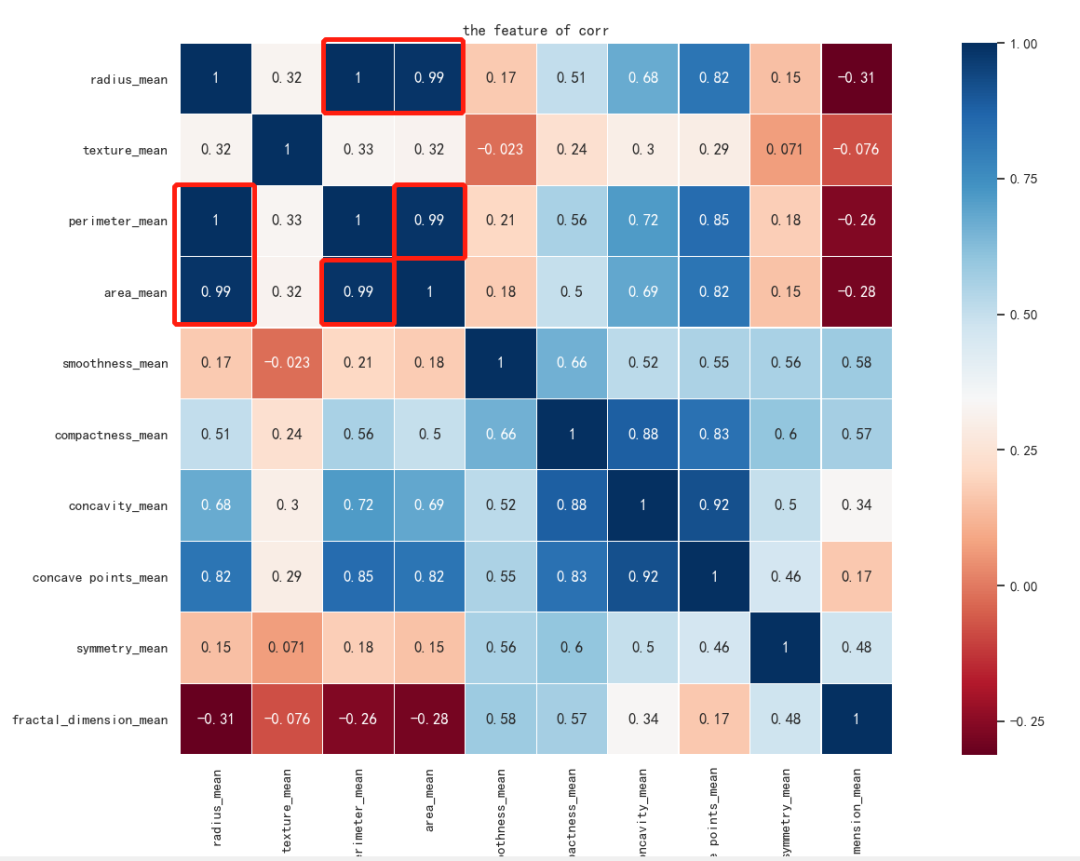
我们发现 radius_mean、perimeter_mean 和 area_mean 这三个特征强相关，那我们只保留一个就行了。这里保留热力�