什么是粒子群优化算法？

粒子群优化算法（Particle Swarm Optimization，PSO）是进化计算的一个分支，是一种模拟自然界的生物活动的随机搜索算法。

PSO模拟了自然界鸟群捕食和鱼群捕食的过程。通过群体中的协作寻找到问题的全局最优解。它是1995年由美国学者Eberhart和Kennedy提出的，现在已经广泛应用于各种工程领域的优化问题之中。

核心思想

粒子群算法是一种仿生算法，模拟鸟群觅食的过程。设想这样一个场景：一群鸟随机搜寻食物，它们一步步地飞，肯定希望离食物越来越近；但是它们不知道食物的方向，只知道当前位置离食物还有多远。这时候，怎么决定飞行的方向呢？不难想到，鸟儿会首先随机飞，积累了经验之后，尽可能往自己曾经到达过的离食物最近的方向上飞；这就是个体学习。

不过，如果鸟儿只是自顾自积累经验的话，那找食物的效率就太低了；为何不大家共享信息互相帮助呢？因此，可以让所有鸟都报告一下自己曾经找到过的离食物最近的距离，在其中找出离食物最近的那一个，然后其他鸟都往那个方向飞；而这就是社会学习。

另外，如果鸟儿仅仅根据自己过去经验中的最优和种群经验中的最优来决定下一步的飞行方向，那么有可能陷入局部最优，也就是失去了全局搜索的能力。因此，我们还希望能有一部分与“最优”无关的因素来决定鸟儿下一步的飞行方向——也就是之前的飞行方向。因此，还需要引入惯性因子，来表征下一步的飞行在多大程度上保留之前的方向。

综上，对于每一只鸟儿来说，每一步的调整需要考虑三个因素：之前的惯性，自己之前的经验，和种群之前的经验。对于粒子群算法来说，每一只鸟（粒子）相当于一个解，鸟儿与食物的距离相当于目标函数值，根据目标函数值计算出适应度；每一只鸟（粒子）有两个属性——速度和位置，位置可以理解为当前解，速度可以理解为每一次迭代中如何调整解。

算法步骤

  1. 初始化：随机给每一个例子设定初始位置和速度。

  2. 计算每个粒子当前的适应度。

  3. 找到个体极值（每一个粒子的历史最优解）和全局最优解（所有粒子的历史最优解）。

  4. 根据个体极值和全局最优解调整速度和位置。

  5. 重复2-4，直到满足终止条件。

    1. 达到设定迭代次数；

    2. 代数之间的差值满足最小界限

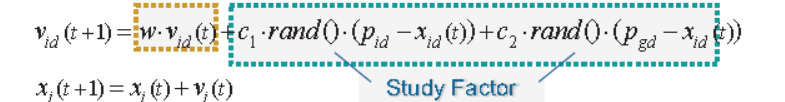
v表示速度，x表示位置。pid表示第i次迭代时的个体极值，pgd表示第i次迭代时的全局最优解。c1是个体学习因子，c2是社会学习因子，w是惯性权重。
v表示速度，x表示位置
pid表示第i次迭代时的个体极值，pgd表示第i次迭代时的全局最优解
c1是个体学习因子，c2是社会学习因子，w是惯性权重

参数设定

群体大小m

  • m很小：陷入局优的可能性很大。

  • m很大：PSO的优化能力很好，当群体数目增长至一定水平时，再增长将不再有显著的作用

惯性因子w

探索是偏离原来的寻优轨迹去寻找一个更好的解，探索能力是一个算法的全局搜索能力。开发是利用一个好的解，继续原来的寻优轨迹去搜索更好的解，它是算法的局部搜索能力。w很小，算法重开发，局部搜索能力强，全局搜索能力弱；w很大，算法重探索，局部搜索能力弱，全局搜索能力强。[1]

学习因子：c1、c2

C1 = 0,无私型粒子群算法，“只有社会，没有自我”但是易迅速丧失群体多样性，易陷于局优而无法跳出

C2 = 0,自我认知型粒子群算法，“只有自我，没有社会”，完全没有信息的社会共享导致算法收敛速度缓慢

C1 C2 都不为0 ，称为完全型粒子群算法。完全型粒子群算法更容易保持收敛速度和搜索效果的均衡，是较好的选择。[2]

最大速度 Vm

作用:在于维护算法的探索能力与开发能力的平衡。

Vm较大时，探索能力增强，但粒子容易飞过最优解·。

Vm较小时，开发能力增强，但容易陷入局部最优。

Vm一般设为没维变量变化范围的10%-20%。

百科介绍

百度百科（详情）

粒子群算法，也称粒子群优化算法或鸟群觅食算法（Particle Swarm Optimization），缩写为 PSO， 是由J. Kennedy和R. C. Eberhart等开发的一种新的进化算法(Evolutionary Algorithm – EA)。

PSO 算法属于进化算法的一种，和模拟退火算法相似，它也是从随机解出发，通过迭代寻找最优解，它也是通过适应度来评价解的品质，但它比遗传算法规则更为简单，它没有遗传算法的“交叉”(Crossover) 和“变异”(Mutation) 操作，它通过追随当前搜索到的最优值来寻找全局最优。这种算法以其实现容易、精度高、收敛快等优点引起了学术界的重视，并且在解决实际问题中展示了其优越性。

粒子群算法是一种并行算法

维基百科（详情）

在计算科学中，粒子群优化（PSO）是一种计算方法，通过迭代地尝试针对给定的质量度量来改进候选解决方案来优化问题。它通过在粒子的位置和速度上根据简单的数学公式得到一组候选解决方案（这里称为粒子）并在搜索空间中移动这些粒子来解决问题。每个粒子的运动受其局部最佳已知位置的影响，但也被引导到搜索空间中最着名的位置，这些位置随着其他粒子找到更好的位置而更新。预计这会将群体推向最佳解决方案。

PSO最初归功于Kennedy，Eberhart和Shi，最初用于模拟 社会行为，作为鸟群或鱼群中有机体运动的程式化表示。该算法被简化并且观察到执行优化。肯尼迪和艾伯哈特的着作描述了PSO和群体智能的许多哲学方面。Poli对PSO应用进行了广泛的调查。最近，Bonyadi和Michalewicz 发表了关于PSO理论和实验工作的综合评论，并回顾了Sengupta，Basak和Peters的历史和近期发展以及杂交观点。

PSO是一种元启发式算法，因为它对被优化的问题做出很少或没有假设，并且可以搜索候选解决方案的非常大的空间。然而，诸如PSO之类的元启发式并不能保证找到最佳解决方案。此外，PSO不使用被优化的问题的梯度，这意味着PSO不要求优化问题可以如经典优化方法（例如梯度下降和准牛顿方法）所要求的那样是可微分的。